trójkąt rownoramienny - analityczna kamil : W trójkącie równoramiennym ABC |AB|=|AC| dane są wierzchołki B=(1,−1), C=(4,0). Jedno z ramion trójkąta zawiera się w prostej x+2y−4=0. Na boku AB obrano taki punkt P że |AP| PB| = 3:2. Znajdź równanie okręgu o środku P i stycznego do boku A

bezendu: Znasz wektory ?

+-: Trójkąt jest równoramienny,a więc symetralna BC (środek BC i prostopadła) przechodzi przez A. Wyznaczasz A=(2,1) Następnie odcinek AB i punkt P zgodnie z warunkami zadania oraz odległość P od prostej, która jest szukanym promieniem.

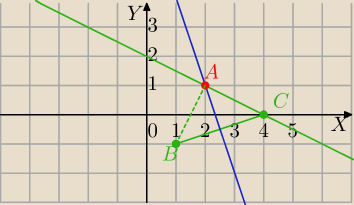
utem: B=(1,−1), C=(4,0). k: x+2y−4=0⇔2y=−x+4

	−1
y=		x+2
	2

	−1
y=		*4+2=−2+2=0 prosta przechodzi przez punktC=(4,0)
	2

BC jest podstawą Δ Symetralna BC jest osią symetrii tego Δ, Symetralna BC jest zbiorem wszystkich punktów jednakowo odległych od punktów B i C P(x,y) punkt symetralnej √(x−1)²+(y+1)²=√((x−4)²+(y−0)²⇔ s: y=−3x+7 równanie symetralnej BC x+2y−4=0 x+2*(−3x+7)−4=0 rozwiąż x=2 y=−3*2+7=1⇔A=(2,1) Oblicz: |AB|, r, .. Dokończysz?