Uprość wyrazenie:
Estrella: Uprość wyrazenie:
√2x + 2√2x − 1 − √2x − 2√2x − 1 , x > 1
31 gru 00:55
Estrella: pomoze ktoś?
31 gru 00:55
bezendu:
Twoja propozycja ?
31 gru 00:55
Estrella: myslalam, zeby moze korzystac z wzorow skroconeo mnozenia, ale szczerze mowiac, nwm jak to
ugryzc
31 gru 00:59
Estrella: bo to mi wylada na jakis wzor,
a2−b2= a2+2ab+b2
31 gru 01:00
Estrella: 2x−1 jest pod pierwiastkiem, tylko nie widac, bo sie zlewa

31 gru 01:01
Estrella: pomozesz

bo zwykle mam jakis pomysl, a tu ani rusz ...
31 gru 01:01
Estrella: plisss
31 gru 01:04
Estrella: nie mam pojecia jak to zrobic, ma ktos jakis pomysl?
31 gru 01:06
Estrella: pomozecie?
31 gru 01:11
Krzyś: dzieki za pomoc, na pewno sobie sama poradze ...
31 gru 01:28
Eta:
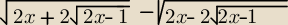
Czy tak wygląda ta liczba?
31 gru 01:29
Eta:
po prawej oznacz k , k>0i podnieś obustronnie do kwadratu
bo dla x>1 lewa strona jest dodatnia
otrzymasz 4x− 4√x2−2x+1= k2
4x−4(x−1)= k2 ⇒ k2=4 , to k=2>0
zatem wartość tej liczby jest równa 2
31 gru 01:32
Eta:
Widzę,że "Krzyś" przemawia głosem .... pani G

31 gru 01:35
pigor: ..., uprościć wrażenie
√2x+2√2x−1− √2x−2√2x−1 , gdzie
x>1
no to np. tak :
niech
√2x+2√2x−1− √2x+2√2x−1 = t /
2 , gdzie
t ≥0 ⇒
⇒ 2x+2
√2x−1 − 2
√ (2x+2√2x−1) (2x−2√2x−1) +2x−2
√2x−1 = t
2 ⇔
⇔ 4x−2
√ (4x2−4(2x−1)= t
2 ⇔ 4x−2
√ 4(x2−2x+1)= t
2 ⇔
⇔ 4x−4
√(x−1)2= t
2 ⇔
t2= 4(x−|x−1|) , ale z założenia x>1 ⇔ x−1>0 ⇒
⇒ t
2= 4(x−(x−1)) ⇔ t
2= 4(x−x+1) ⇔ t
2= 4 i t ≥0 ⇒
t=2 , czyli
√2x+2√2x−1− √2x+2√2x−1 =2 . ...

31 gru 01:35
pigor: ...,

31 gru 01:37
Eta:


31 gru 01:45
5-latek: A kto to jest Pani G ?
31 gru 01:46
5-latek: A to ta Pani ? Niech tam sobie zyje
31 gru 01:49
Eta:
Nie mylić z Mateuszem G

31 gru 01:51
5-latek: Widzisz
Eta to ja jednak nie jestem w temacie .
U nas na wsi sie o takich sprawach nie rozmawia

31 gru 01:54
Estrella: dzieki za pomoc

31 gru 01:55
Eta:
Z "małolatami" się o tym nie rozmawia

31 gru 01:55
Estrella: o jaka pania G codzi?
31 gru 01:56
31 gru 01:56
5-latek: 
31 gru 01:58
31 gru 01:58
Eta:
Dobrej nocki Wszystkim

31 gru 02:01
Estrella: Wzajemnie

31 gru 02:06

 bo zwykle mam jakis pomysl, a tu ani rusz ...
bo zwykle mam jakis pomysl, a tu ani rusz ...
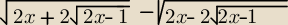 Czy tak wygląda ta liczba?
Czy tak wygląda ta liczba?












