,
RS:
Napisz równanie okręgu, którego środek znajduje się na prostej k , przechodzącego przez punkty
A i B , jeśli k :y =−2x−2; A(5 ,10), B (3,12)
30 gru 21:54
Saizou :
odległość
AS=BS=r , gdzie S to środek okręgu i S(x;−2x−2)
, zatem....
30 gru 21:57
devo:
o: (x+3)
2+(y−4)
2= 100
30 gru 22:05
RS:
Ale jak to rozwiązać ?
30 gru 22:07
devo:
Prosto
rozwiązać równanie jakie podał Ci
Saizou
30 gru 22:09
RS:
Czyli wzór na długość odcinka
?
30 gru 22:10
devo:
taaaaaaaaaaaaaaaaak
30 gru 22:12
RS:
Już rozwiązałem.
30 gru 22:14
devo:
30 gru 22:15
Saizou : nie taki diabeł straszny jak go malują
30 gru 22:23
Saizou : 
na Sylwestra
30 gru 22:25
devo:
a może
30 gru 22:32
RS:
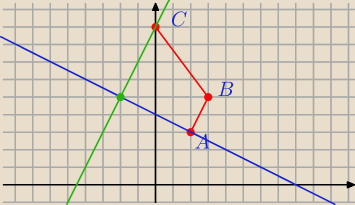
prosta AD:y=−0,5x+4
prosta CD:y=2x+9
i z punktu przecięcia się tych prostych mam punkt D=(−2,5) ?
30 gru 22:41
RS: a tutaj polecenie:
Dane są punkty A = (2,3),B = (3,5) i C = (0 ,9) . Wyznacz współrzędne punktu D , dla którego
czworokąt ABCD jest trapezem prostokątnym, którego kąt przy wierzchołku A jest prosty
30 gru 22:44
RS: ?
30 gru 23:15
daras: Remanent
31 gru 07:04
utem:
1) prosta AB:
A = (2,3),B = (3,5)
y=ax+b
3=2a+b
5=3a+b odejmuję stronami
−2=−a
a=2
AB: y=2x+b ( b − nie jest nam potrzebne)
Dalej dobrze.
31 gru 16:27