k
RS:
Na prostej y =−x wyznacz punkt, który jest równo odległy od początku układu współrzędnych oraz
od punktu P=(−2,3)
y=−x
x+y=0
| | √2 | |
d=U{|−2+3+0|}{√2= |
| a dalej ? |
| | 2 | |
30 gru 19:08
30 gru 19:08
Kaja: ten punkt ma postać (x,−x). niech ten punkt nazywa się A.
wtedy |AO|=|AP|, gdzie O=(0,0)
zastosuj wzór na odległośc między dwoma punktami (taki z pierwiastkiem)
30 gru 19:10
devo:
|AO|2= |AP|2 , O(0,0), A(x,−x)
30 gru 19:20
RS:
| | √2 | |
@Kaja to będzie tak √(x−0)2+(−x−0)2= |
| /2 |
| | 2 | |
4x
2=1
30 gru 19:23
30 gru 19:24
kaka:
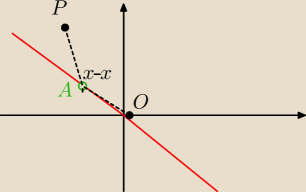
30 gru 19:25
RS:
odległość punkt p od prostej
30 gru 19:25
RS:
to czemu w poście 19:08 jest błąd ?
30 gru 19:27
RS: ?
30 gru 19:30
devo:
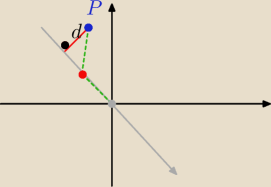
30 gru 19:30
Kaja: no właśnie,ta odległość o którą chodzi to niekoniecznie ta najkrótsza
30 gru 19:31
devo:
Wiesz już dlaczego?
30 gru 19:32
RS:
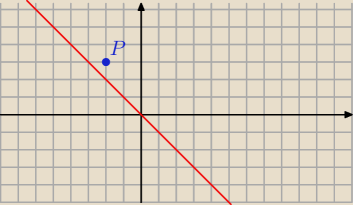
y=−x
x+y=0 równanie ogólne prostej
P(−2,3)
| | |−2+3+0| | | 1 | | √2 | |
d= |
| = |
| = |
| co nie tak / |
| | √2 | | √2 | | 2 | |
30 gru 19:32
Kaja: a ten wzór z wartością bezwzględną jest tak jakby na ta najkrótsza odległość, czyli tak jakbys
sobie przeprowadził przez ten punkt prostą prostopadłą do danej prostej
30 gru 19:33
Kaja: mnie wyszedł inny wynik
30 gru 19:34
devo:
Taki masz Kaja ? A( −1,3; 1,3)
30 gru 19:35
RS:
Punkt A=(x,−x)
AO=AP
4x
2=1

30 gru 19:35
devo:

30 gru 19:36
RS:
Czemu ?
30 gru 19:37
Kaja: nie devo
30 gru 19:38
devo:
| | 1 | | 1 | |
Zaznacz ten punkt( |
| , − |
| ) i zobaczysz,że to nie jest ten o który chodzi  |
| | 2 | | 2 | |
30 gru 19:38
RS:
No tak. To czemu stosujemy inny wzór ? Proszę o wytłumaczenie.
30 gru 19:39
devo:
Jak nie: x2+x2=(x+2)2+(−x−3)2
4x+6x= −13
x= −1,3 to A( −1,3;1,3)
30 gru 19:40
Kaja: devo masz racę, brakowało mi minusa przed x

30 gru 19:42
RS: 19:39 ?
30 gru 19:44
RS: ?
30 gru 19:51
Kaja: RS zobacz 19:33
30 gru 19:51
devo:
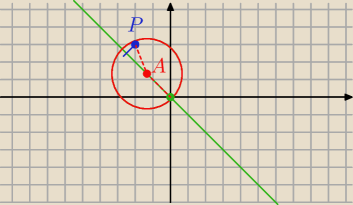
Szukany punkt A jest środkiem okręgu gdzie r= |PA|=PO|
A odległość P od prostej ≠ r
30 gru 19:52
RS:
Czy wszystko musi opierać się na tych okręgach ?
30 gru 19:54
Kaja: RS, a co kręci ci się już w głowie

?
30 gru 19:56
devo:

Tak by było gdyby punkt P leżał na osi OY wtedy r= d
30 gru 19:57
devo:
Hehe ....... pewnie już szampana "degustował"

Oczywiście żartuję

30 gru 19:58
Kaja: 
30 gru 19:59
RS:
Nie spożywam %

Nawet w sylwestra.
30 gru 20:00
Kaja: abstynent?

30 gru 20:02
RS:

Szkoda mi zabijać szare komórki przed maturą

30 gru 20:03
devo:
Wypijesz swoje....... jak zostaniesz
chirurgiem 
Każdy chirurg ... popija ( znam to z autopsji )

30 gru 20:04
RS:
Ale spirytus jest mocniejszy

30 gru 20:04
Kaja: a co devo , chirurgiem jesteś?

30 gru 20:05
devo:

30 gru 20:05
RS:
''matematycznym'' zapewne

30 gru 20:05
devo:
Prawie tak

30 gru 20:05
Kaja: nie napiszesz ?

30 gru 20:05
Kaja: czyli?

30 gru 20:06
Kaja: nie bądź taki tajemniczy devo

30 gru 20:06
RS:
To Eta jest przecież

Kaja a wracając do zadania nie można obliczać odległości punktu od prostej ?
30 gru 20:08
Kaja: RS a przeczytałeś to co ja pisałam wcześniej?

ten wzorek jest przecież na najkrótsza
odległość, czyli tak jakbyć poprowadził przez ten punkt prosta prostopadłą do danej prostej.
ty w rzeczywistość nie wiesz czy to będzie ta najkrótsza odległość.
30 gru 20:11
Kaja: to jeśli to Eta, to czemu ma inny nick?

ukrywa się?

30 gru 20:12
RS:
Kobi
Eta zmienną jest ?

30 gru 20:14
devo:

30 gru 20:15
Kaja: RS jak to pięknie wykombinowałeś


30 gru 20:17
RS: 
30 gru 20:18
RS:
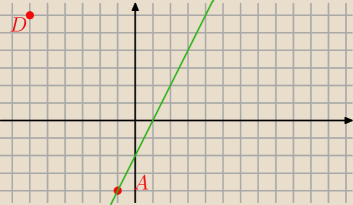
Oblicz pole i obwód rombu ABCD wiedząc, że przekątna AC jest zawarta w prostej o równaniu
y=2x−2 oraz A=(−1,−4) i D=(−6,6) .

proszę o wskazówkę ?
30 gru 20:24
devo:
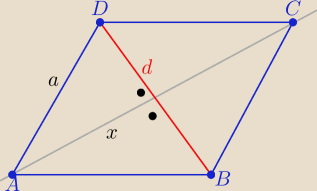
Jeden ze sposobów

Ob= 4a=4|AD|=..........
P= 2x*d=....
d−−− odległość D od prostej AC i x −−−−− z tw, Pitaorasa
30 gru 20:38
devo:
Oznaczam
d−−− połowa krótszej przekątnej
30 gru 20:40
RS:
Dziękuję, zaraz będę analizował.
30 gru 20:44
devo:
To jest zadanie na
podstawę 
30 gru 20:52
RS:
To tak. Ale ja robię wszystkie zadania z analitycznej, muszę się doszkolić. A masz jeszcze inny
sposób ?
30 gru 20:53


 y=−x
x+y=0 równanie ogólne prostej
P(−2,3)
y=−x
x+y=0 równanie ogólne prostej
P(−2,3)




 Szukany punkt A jest środkiem okręgu gdzie r= |PA|=PO|
A odległość P od prostej ≠ r
Szukany punkt A jest środkiem okręgu gdzie r= |PA|=PO|
A odległość P od prostej ≠ r
 ?
?
 Tak by było gdyby punkt P leżał na osi OY wtedy r= d
Tak by było gdyby punkt P leżał na osi OY wtedy r= d
 Oczywiście żartuję
Oczywiście żartuję 

 Nawet w sylwestra.
Nawet w sylwestra.

 Szkoda mi zabijać szare komórki przed maturą
Szkoda mi zabijać szare komórki przed maturą 
 Każdy chirurg ... popija ( znam to z autopsji )
Każdy chirurg ... popija ( znam to z autopsji ) 








 Kaja a wracając do zadania nie można obliczać odległości punktu od prostej ?
Kaja a wracając do zadania nie można obliczać odległości punktu od prostej ?
 ten wzorek jest przecież na najkrótsza
odległość, czyli tak jakbyć poprowadził przez ten punkt prosta prostopadłą do danej prostej.
ty w rzeczywistość nie wiesz czy to będzie ta najkrótsza odległość.
ten wzorek jest przecież na najkrótsza
odległość, czyli tak jakbyć poprowadził przez ten punkt prosta prostopadłą do danej prostej.
ty w rzeczywistość nie wiesz czy to będzie ta najkrótsza odległość.
 ukrywa się?
ukrywa się?





 Oblicz pole i obwód rombu ABCD wiedząc, że przekątna AC jest zawarta w prostej o równaniu
y=2x−2 oraz A=(−1,−4) i D=(−6,6) .
Oblicz pole i obwód rombu ABCD wiedząc, że przekątna AC jest zawarta w prostej o równaniu
y=2x−2 oraz A=(−1,−4) i D=(−6,6) .
 proszę o wskazówkę ?
proszę o wskazówkę ?
 Jeden ze sposobów
Jeden ze sposobów  Ob= 4a=4|AD|=..........
P= 2x*d=....
d−−− odległość D od prostej AC i x −−−−− z tw, Pitaorasa
Ob= 4a=4|AD|=..........
P= 2x*d=....
d−−− odległość D od prostej AC i x −−−−− z tw, Pitaorasa
