najmniejsza wartość Lemon: Znajdź najmniejszą wartość

	m2+3m−2
f(m) =		w przedziale m ∊ <2;4>
	m2+1

Próbowałem takim sposobem, aby odnaleźć najmniejszą wartość funkcji w liczniku oraz największą wartość funkcji z mianownika w podanym przedziale. Wtedy ułamek będzie najmniejszy. Ale nie dostaję prawidłowego wyniku. Dlaczego?

john2: Hmm, tylko jak znaleźć największą wartość m² + 1? Proponuję pochodną, jak Jakub zrobił https://matematykaszkolna.pl/strona/1332.html

john2: Aha jest m∊<2,4>, więc może się da.

Lemon: No da się, ale zły wynik wychodzi.

Lemon:

26
	wychodzi jak policzy się największe wartości tych funkcji przedziale <2,4>
17

Lemon: Mógłby ktoś się odnieść dlaczego moje rozumowanie jest złe?

john2: Dołączam się do pytania. Twój pomysł brzmi logicznie, ale ja sobie to tłumaczę tak, że nie możemy "rozerwać" tej funkcji i badać dwóch funkcji kwadratowych osobno. Brakuje mi tu tej "łączności" między licznikiem a mianownikiem. http://www.wolframalpha.com/input/?i=plot+%28m^2+%2B+3m+-+2%29%2F%28m^2+%2B+1%29 Mam wrażenie, że to tak, jakby próbować ten wykres jakoś podzielić na dwie parabole. Sorry, że nie odpowiem na Twoje pytanie fachowo. Trochę zbyt ambitne na mnie się okazało.

Lemon: Chyba masz rację Ale poczekajmy, może ktoś jeszcze się wypowie.

Bizon:

	8
chyba raczej
	5

Bizon: ... przepraszam ... pytają o najmniejszą −

john2:

	8
No właśnie. Wychodzi mi najmniejsza wartość =		, gdy robię to sposobem Lemona. Ciekawi
	5

mnie, jak wytłumaczyć niepoprawność tego sposobu.

Lemon: up

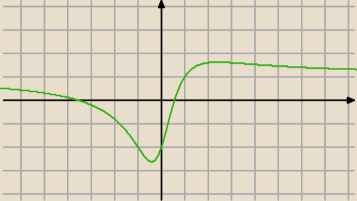
Bizon: ... chyba raczej bez pochodnych trudno będzie Tym bardziej, że funkcja w badanym przedziale ma ekstremum (maximum) A z pochodnymi ... banał

Bogdan: Określimy najpierw monotoniczność funkcji f(m) w przedziale A = <2, 4>. Założenia: m₁∊A i m₂∊A i m₂ − m₁ > 0 Wyznaczamy znak różnicy: f(m₂) − f(m₁)

	m22 + 3m2 − 2		m12 + 3m1 − 2
f(m2) − f(m1) =		−		=
	m22 + 1		m12 + 1

	(m22+3m2−2)(m12+1) − (m12+3m1−2)(m22+1)
=		= ... < 0
	(m22+1)(m12+1)

Funkcja f(m) w przedziale A = <2, 4> jest malejąca, największa wartość jest równa f(2) = 8/5, najmniejsza f(4) = 26/17

Bizon: ... to chyba nie całkiem prawda Bogdanie Funkcja w tym przedziale monotoniczna nie jest ! dla m=1+√2 ma max

Bogdan: Prawda Bizon, jest maksimum w tym przedziale, dziękuje za poprawienie.

Bizon:

	(2m+3)(m2+1)−2m(m2+3m−2)		−3m2+6m+3
f'(m)=		=
	(m2+1)2		(m2+1)2

warunek konieczny −3m²+6m+3=0 ⇒ m²−2m−1=0 m₁=1−√2 m₂=1+√2 min max Teraz sprawdzamy na krańcach przedziału .... i wnioski

Bizon: − ... zdarza się ...

Lemon: Doceniam Wasze starania, ale mi naprawdę nie chodziło o rozwiązanie tego zadania, bo takowe mogę znaleźć używając googli Gdyby ktoś mógł mi wskazać ułomność mojego rozumowania z pierwszego postu, będę niezmiernie wdzięczny

Bizon: ...tego Twego pytania (rozumowania) nie idzie nawet "ocenić" Chcesz znaleźć największą wartość licznika i najmniejszą mianownika ... i jeszcze zupełnym przypadkiem miałoby to "zachodzić" dla tego samego m −

Lemon: Chodziło mi właśnie o skomentowanie tego pomysłu, dziękuję. Ale mogłeś od razu to napisać

Bizon: sądziłem, że szukasz rozwiązania a nie komentowania −

Lemon:

Bizon: skąd to zadanie?

Lemon: matura, bodajże 2007

Bizon: czyli z pochodnymi −

Lemon: Wtedy były, teraz znowu wprowadzili, a mój rocznik nie ma Dlatego kombinowałem jakby to rozwiązać bez pochodnych. Teraz widzę, że pomysł nie był najwyższych lotów. Ile czasu potrzeba na ogarnięcie pochodnej? Tak mniej więcej?

Bizon: ... to nie tylko liczenie pochodnych To bardziej umiejętność analizy przebiegu zmienności funkcji ... czyli wykorzystanie i interpretowanie −

Bizon: tydzień −

Lemon: To na razie sobie odpuszcze. Lepiej tydzień dłużej robić zadania maturalne, pochodna niezbędna nie jest w tym momencie.

Bizon: −

utem: Nie możesz stwierdzić czy iloraz tych funkcji jest w przedziale <2,4> jest funkcją monotoniczną. Do tego trzeba wykorzystać własności pochodnej.