cc Oll: Z wierzchołków prostokąta poprowadzono proste prostopadłe do jego przekątnej. Proste te dzielą przekątną na trzy równe części, każda o długości 5 cm. Oblicz pole i obwód prostokąta.

pigor: ..., np. tak, niech h − dł. odcinka prostopadłego do przekątnej , a x,y − długości krótszego i dłuższego odpowiednio boku prostokąta, to P=xy=? − szukane pole i O=2(x+y)=? obwód prostokąta, więc z podobieństwa 3−ech ΔΔ prostokątnych (cecha kkk) np.nad przekątną prostokąta mamy układ ^x_y= ⁵_h= ^h₁₀ ⇒ h²=5*10 i ^x_y= ^h₁₀ ⇔ ⇔ h=5√2 i 10x=5√2y ⇒ 2x= √2y ⇔ 4x²=2y² ⇔ (*) y²=2x² a z tw. Pitagorasa x²+y²= 15² ⇒ 3x²= 15*15 ⇔ ⇔ x²= 5*15=75= 25*3 i z (*) y²= 25*6 ⇒ x=5√3 i y=5√6 , zatem P= xy= 5√3*5√6= 25√18=50√2 [cm²] − szukane pole prostokąta, zaś O= 2(x+y)= 2(5√3+5√6)= 10(√3+√6) = 10√3(1+√2) [cm] − szukany jego obwód . ...

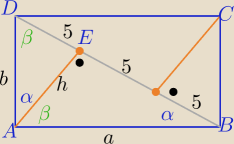
Eta: |BD|=15 z podobieństwa trójkątów ABE i AED

	h		10
		=		⇒ h= 5√2 to P(prostokąta)= h*|BD|= .... =75√2 cm2
	5		h

b= √50+5²= 5√3 , a= √50+10²=5√6 Ob= 2a+2b=.......

Eta: Hehe... U mnie mniej kolorowo ale z rysunkiem

5-latek: Eta ale u Ciebie jest wiecej kolorow bo u pigora nie ma zielonego

Eta: I pomarańczowego

pigor: ... , o bardzo ładnie się ... uzupełniamy, ale ... coś pole nam się nie

Eta: Ejjj pigor ....... 5√3*5√6= .........= ? ( piłeś coś?

pigor: ... , niestety, najgorsze, to to, że dzisiaj NIC z tych rzeczy