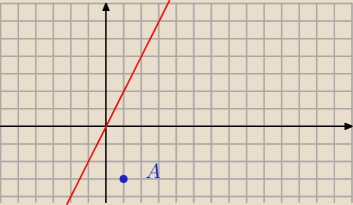
l RS: kwadrat ABCD ma dane są wierzchołek A (1,−3) i równanie prostej k 2x−y=0 w której zawiera się jedna z przekątnych kwadratu. Znajdź współrzędne wierzchołka C oraz oblicz pole tego kwadratu Odległość Punktu A od prostej jest równa punktowi C wyznaczyłem A 2x−y=0 A(1,−3)

	|2+3+0|		5		5√5
d=		=		=		=√5
	√5		√5		5

|2x−y|
	=√5
√5

|2x−y|=5 co dalej ?

pigor: ..., nie wiem skąd i dlaczego, ale to |2x−y|=5 ⇔ 2x−y= −5 v 2x−y= 5 ⇔ 2x−y+5=0 v 2x−y−5= 0 − dwie proste równoległe

RS: A czemu to jest źle ?

MQ: Skoro A nie leży na prostej, to dwa punkty kwadratu są przecięciem okręgu o środku w A i promieniu √2d. Trzeci punkt jest symetryczny do A wzgl. prostej.

RS: MQ ale czemu mój pomysł nie jest poprawny ?

MQ: Nic nie pisałem o twoim sposobie. To równanie, które otrzymałeś, to równanie na wszystkie punkty odległe od prostej 2x−y=0 na dystans √5, czyli, jak zauważył pigor, równania dwu prostych równoległych do 2x−y=0. Na jednej leży A, a na drugiej C.

5-latek: Wczoraj rozwiazylaes podobne zadanie gdzie pytales o jednolkadnosc Mozna to rozwiazac tak −ja bym tak rozwiazal napisal rownanie prostej prostopadlej do postej k i przechodzacej przez punkt A Da mi to rownanie drugiej przekatnej bo przekatne w kwadracie przecinaja sie pod katem prostym Wyznaczyl punkt przeciecia sie prostych ktory bedzie srodkiem odcinka AC ze wzoru na srodek odcinaka wyznaczyl wsplrzedne punktu C AC to przekatna wiec wiadomo co dalej

MQ: Jak widzę, 5−latek daje rozwiązanie prostymi, ja −− okręgami. Masz więc już dwa sposoby.

5-latek:

RS: Dzięki Panowie.