,
RS:
Dany jest ΔABC, gdzie |∡ACB |=90, wierzchołek B ma współrzędne (6,0) . Prosta p:11x+2y−6=0,
zawierająca środkową trójkąta poprowadzoną z wierzchołka C , przecina bok AB trójkąta w
punkcie S =(1;−2.5) . Wyznacz współrzędne punktów A i C
Punkt A wyznaczyłem biorąc, że S jest środkiem odcinka |AB| otrzymałem współrzędne A=(−4,−5)
Ale nie wiem jak wyznaczyć wsp punktu C ?
29 gru 20:19
gusia: środkowa opuszczona na przeciwprostokątną dzieli trójkąt na dwa trójkąty równoramienne....
może to cię trochę naprowadzi... albo coś pomoże...
29 gru 20:35
utem:
1)S=(1;−2,5) r=|SB|=√(6−1)2+(−2,5)2=√25+6,25=√31,25
Rozwiązujesz układ :
(x−1)2+(y+2,5)2=31,25 i 11x+2y−6=0
2) sposób
C=(x;−5,5x+3)
|AC|2+|BC|2=|AB|2
Napisz wyniki
29 gru 20:39
RS:
To wiem, ale nijak to ma się do mojego zdania. Tu jest coś z prostymi potrzebne (chyba)
29 gru 20:39
utem:
RS, co to za tekst?
To,że nie rozumiesz co do Ciebie "mówię', to nie znaczy, że źle Ci podpowiadam.
Podobne zadanie już rozwiązywaliśmy.
29 gru 20:44
RS:
A ja kogoś oskarżam o złe podpowiedzi ? A po drugie ta wypowiedź była skierowana dla gusi. I
rozumiem co do mnie mówisz.
29 gru 20:48
utem:
To jak, zrobione, czy zacząć?
29 gru 21:00
RS:
Nie zrobione.
29 gru 21:01
utem: Już piszę.
29 gru 21:02
utem:
1)
(x−1)
2+(y+2,5)
2=31,25 i 11x+2y−6=0⇔y=−5,5x+3
x
2−2x+1+(−5,5x+3+2,5)
2=31,25
Rozwiąż
29 gru 21:09
RS:
x2−2x+1+30,25x2−60,5x+30,25=31,25 /4
4x2−8x+4+121x2−242x+121=125
125x2−250x=0 /125
x2−2x=0
x(x−2)=0
x1=0 lub x2=2
y1=3 lub y2=−8
?
29 gru 21:15
utem:
II sposób
Z Tw. Pitagorasa:
C(x,−5,5x+3)
A=(−4,−5)
B=(6,0)
AB2=AC2+BC2
(6+4)2+(0+5)2=(x+4)2+(−5,5x+3+5)2+(x−6)2+(−5,5x+3)2
125=x2+8x+16+(−5,5x+8)2+x2−12x+36+30,25x2−33x+9
dokończ
29 gru 21:20
RS: Z pitagorasa wychodzi to samo. Tylko wyjaśnij proszę czemu akurat to zadanie kojarzone jest z
okręgiem ?
29 gru 21:21
utem: 21:15
Dobrze.
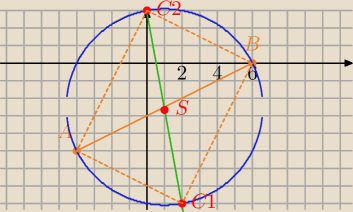
C1=(0,3)
C2=(2,−8)
Wykorzystano, że środek okręgu opisanego na Δ prostokatnym leży w środku przeciwprostokatnej i
kąt wpisany oparty na średnicy jest prosty.
29 gru 21:22
RS:
Czyli wszystkie trójkąty które będą miały kąt prosty mogę rozwiązać korzystając z równania
okręgu
?
29 gru 21:24
utem:
Pewnego typu tak, ale musisz uważać, gdzie ma być kąt prosty.
29 gru 21:30
RS:
Na przeciwprostokątnej. Dzięki za pomoc.
29 gru 21:32