objętośc ostrosłupa
gusia: Obliczyć objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy długości 3 i kącie
o mierze 60 stopni między dwoma sąsiednimi ścianami.
Śiedzę nad nim pól dnia i wychodzą mi dziwne wyniki więc nie wiem czy wogóle zadanie jest do
rozwiązania. Będę wdzięczna za pomoc
29 gru 20:10
dero2005:
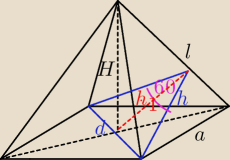
a = 3
d = a
√3 = 3
√3
d
2 = 2h
2 − 2h
2cos 60
o
27 = 2h
2( 1 −
12)
27 = h
2
h = 3
√3
h
1 =
√h2 − (d2)2 =
92
H = l
√3
H
2 = l
2 − (
d2)
2
3l
2 = l
2 − (
3√32)
2
8l
2 = −27 → sprzeczność
kąt zawarty pomiędzy sąsiednimi ścianami ostrosłupa o podstawie kwadratu powinien się zawierać
90<α<180, teoretycznie gdyby wysokość dążyła do ∞ to byłby graniastosłup i kąt byłby 90
o a
gdyby wysokość dążyła do 0 to boki "złożyłyby" się na podstawie i byłby 180
o
29 gru 21:56
gusia: właśnie też w swoich obliczenich miłam minusową liczbę i myślałm że coś pomyliłam.... super i
dzięki za odpowiedź
29 gru 22:11
Bizon:
... ciekawe te "rachunki"
Już na starcie ... skoro d jest przekątną kwadratu o boku a=3
to na pewno d≠3√3 ... i dalej "paszło" −:(
29 gru 23:16
Bizon:
| | H | | h1 | |
... o "podobieństwie" trójkątów i proporcji |
| = |
| ... już nie wspomnę |
| | l | | d/2 | |
29 gru 23:27
gusia: ja przeanaizowałam i wydaje mi się to dobrze rozwiązane... ale jeżeli masz inną propozycję to
podaj
30 gru 09:54
Bizon:
... a co Ty przeanalizowałaś
?
1. Skoro w podstawie masz kwadrat o boku 3 ... to jego przekątna jest 3
√3 ?
2. Jeśli kąt dwuścienny miałby mieć 60
o ... to "wyliczanie" h i h
1 ... to zbędna zabawa.
Wiadomo, że trójkąt zaznaczony na rysunku "na niebiesko" jest równoboczny
| | 3√2√3 | | 3√6 | |
zatem h=d=3√2 zaś h1= |
| = |
| |
| | 2 | | 2 | |
Dalej poprawiaj sama bo niestety wyliczenia
dero2005 to jedna wielka sprzeczność −
30 gru 10:07
gusia: oddaję honor
ja jako blondynka nie zauważyłam tych wpadek i byłam szczęśliwa że ktoś pomógł
mi z zadaniem
dzięki
30 gru 11:16