pl RS: Punkty B = (0,10) i O=(0,0) są wierzchołkami trójkąta prostokątnego OAB,w którym |∡OAB | = 90^∘

	1
.Przyprostokątna OA zawiera się w prostej o równaniu y=		x .Oblicz współrzędne punktu A
	2

	1
prosta OA =		x i teraz prostopadła do niej i przechodząca przez punkt B y=−2x+10
	2

Z resztą sobie poradziłem. Macie jakieś inny pomysł na to zadanie ? Jestem ciekawy innych rozwiązań ?

RS: ?

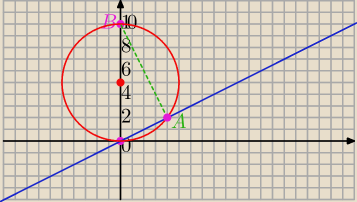
utem: S=(0,5) − środek OB x² +(y−5)²=5² równanie okręgu o środku S(0,5) i r=5 ∡OAB=90^o jako wpisany w okrąg oparty na średnicy. Po rozwiązaniu układu równań , otrzymasz wsp. punktu A

	1
x2 +(y−5)2=25 i y=		x
	2

RS: Punkt A (4,−10) jest wierzchołkiem równoległoboku ABCD . Dwa boki równoległoboku zawierają się w prostych o równaniach y=3x−2 i y=−x+6 . Wyznacz pozostałe wierzchołki równoległoboku Mogę policzyć punkt przecięcia się prostych ale co on da ? Nie wiem czy to będzie punkt D ? Jeśli byłby to D to miałbym tylko punkt symetrii ale co dalej ?

pigor: ... np. tak : z warunków zadania A=(x,y) i A∊ y=¹₂x ⇒ A=(2y,y)=? , to z tw. Pitagorasa : |OA|²+|AB|²= |BO|² ⇔ (2y)²+y²+(−2y)²+(10−y)²= 10² ⇔ ⇔ 9y²+10²−20y+y²= 10² ⇔ 10y²−20y= 0 /:10y>0 ⇒ ⇒ y−2=0 y=2 , więc x=2y=4 , zatem A=(4,2}− szukany punkt. ...

pigor: ... lub z iloczynu skalarnego : AB^→⊥ AO^→ ⇔ [−2y,−y] ◯ [−2y,10−y]= 0 ⇔ 4y²−y(10−y)= 0 ⇔ ⇔ 4y²−10y+y²=0 ⇔ 5y(y−2)=0 i y>0 ⇔ y=2 ⇒ A=(2y,y)=(4,2).

pigor: ... lub z iloczynu skalarnego : AB^→⊥ AO^→ ⇔ [−2y,−y] ◯ [−2y,10−y]= 0 ⇔ 4y²−y(10−y)= 0 ⇔ ⇔ 4y²−10y+y²=0 ⇔ 5y(y−2)=0 i y>0 ⇔ y=2 ⇒ A=(2y,y)=(4,2).

5-latek: pigor A ma dany

pigor: ?. przepraszam za ten dubel

pigor: wydaje mi się , że RS myśli o rozszerzeniu a więc ...

RS: A jakieś inne propozycje ? Do rozwiązań pigora jeszcze ''nie dorosłem''.

RS: @piogr tak myślę o rozszerzeniu, ale rachunek wektorowy to coś co omijam szerokim łukiem. Wiem, że muszę się tego nauczyć,ale..

utem: Rozwiązałeś 18:52? Rozwiązałeś 19:01 ? tam nie ma wektorów. To dobre sposoby.

RS: 18:52 A=(4,2) 19:01 też rozwiązałem chodzi o zadanie 18:55 ? Wskazówkę

utem: Rysunek 1) punkt przecięcia prostych to drugi wierzchołek 2) piszesz równanie prostej równoległej do prostej y=−x+6 i przechodzącej przez A(4,−10), punkt przeciecia z prostą y=3x−2 to trzeci wiezrchołek 3) piszesz równanie prostej równoległej do prostej y=3x−2i przechodzącej przez A(4,−10), punkt przeciecia z prostą y=−x+6 to następny wierzchołek wierzchołek

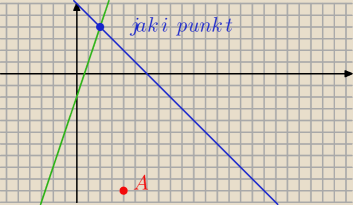
RS: Wyznaczyłem punkt przecięcia się prostych ale skąd mam wiedzieć który to punkt ?

pigor: ..., Punkt A (4,−10) jest wierzchołkiem równoległoboku ABCD . Dwa boki równoległoboku zawierają się w prostych o równaniach y=3x−2 i y=−x+6 . Wyznacz pozostałe wierzchołki równoległoboku . −−−−−−−−−−−−−−− no to np. tak A=(4,−10)∊ (AB: 3x−y+C=0 v AD: x+y+C=0) , gdzie AB || CD: 3x−y−2=0 , a AD || BC: x+y−6=0 ⇒ (AB: 3*4+10+C=0 v [c[AD: 4−10+C=0) ⇒ ⇔ (AB: C= −22 v AD: C= 6) ⇒ (AB: 3x−y−22=0 v AD: x+y+6=0) − równania boków (brakujące) równoległoboku , więc szukane wierzchołki to punkty przecięcia się boków: B=(x,y): AB i BC v C=(x,y): BC i CD v D=(x,y): AD i CD ⇔ ⇔ B: (3x−y=22 i x+y=6) v C: (x+y=6 i 3x−y=2) v D: (x+y= −6 i 3x−y=2) ⇔ ⇔ B: (4x=28 i y=6−x) v C: (4x=8 i y=6−x) v D: 4x= −4 i y= −x−6) ⇔ ⇔ B: (x=7 i y=−1) v C: (x=2 i y=4) v D: x= −1 i y= −5) ⇔ ⇔ B=(7,1) v C=(2,4) v D=(−1,−5) i to by było tyle ... −−−−−−−−−−−−−−−−−−−− nie sprawdzam, obym się nie ...

pigor: ... , a do mojego rozwiązania to się nie uprzedzaj z góry, bo jest elementarne i o tym mówi ci utem w swoim poście, cóż mój zapis ci nie odpowiada, tak

RS: Właśnie tak.

utem: Co to znaczy jaki punkt? Wierzchołek C. 3x−2=−x+6 x=2 y=4 C=(2,4) Dalej rozwiązuj.

RS: Właśnie o to mi chodzi, że skąd pewność w przecięciu tych prostych jest punkt C a nie B albo D. Dlatego napisałem ''jaki punkt''

utem: Naszkicuj równoległe do danych prostych i przechodzące przez A. Nie widzę innej opcji.

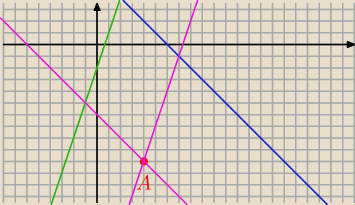
RS: Narysowałem,.

RS: I dopiero teraz to zauważyłem ale jak na to wpaść od razu bez zbędnego rysowania ?

5-latek: RS przeciez to jest geometria analityczna . Ale geometria. W geomertrii najwazniejszy jest rysunek . CO zescie sie tak nauczyli robic bez rysunku a potem plakac Nie mialem zamiaru sie wtracac . A nawet gdybys zaznaczyl ten punkt B czy D to przeciez TY rozwiazujesz zadanie i w kazdej chwili mozesz to porawic no wlasnie majac rysunek

RS: No wiem, że analityczna i rysunek jest ważny, ale utem widział to bez rysunku ?

utem: Tak właśnie, jak pisze 5−latek, Rysunek to podstawa w geometrii.

RS: Dobra. Dzięki za pomoc. Wiem, że robiąc rysunek bardzo dużo można wywnioskować

pigor: ..., no właśnie rys pomocniczy nawet odręczny i wcale nie musi być w XOY, jest jednak niezbędny by nanosić na nim dane itp wg uznania np. równania danych prostych, bo wtedy mając taki rys "jedź" od punktu A w kierunku przeciwnym do ruchu zegara i masz kolejne wierzchołki brakujące BCD i ty szukasz prostych zawierających boki tego równoległoboku; ja w skrócie te proste i ch równania oznaczam w swoim poście jako boki AD AB,BC,CD, dlatego nie podchodź do mojego rozwiązania "jak do jeża" i czytaj jednak go krok, po kroku, słowo po słowie i dorysowuj to o czym kolejno piszę wtedy to mój tak skondensowany opis będzie ci zrozumiały i tym samym całe proste rozwiązanie

pigor: ...tak wywnioskować można z rysunku, ale uważaj na "pochopne" wnioski z niego, bo dopiero analityczne (rachunkowe) uzasadnienie tego co "widzisz" jest rozwiązaniem tego ...

RS: Tak wiem, czasami wydaję sie tyle a w obliczeniach wychodzi coś innego.