matura ewa: p unktya(2,c0) ib(12,0)sa wierzcholkami trojkata prostokatnego abc o przeciwprostokatnej ab. wierzcholek c lezy na prostej o rownaniu y=x.oblicz wspolrzedne punktu c

utem: A(2,0) B(12,0) C∊k, gzie k: y=x Takie są dane?

ewa: tak

Janek191: A = ( 2; 0) B = ( 12; 0) C = ( x; x) Tw. Pitagorasa I AB I ² = I AC I² + I BC I² ; I AB I = 12 − 2 = 10 10² = ( x − 2)² + ( x − 0)² + ( x − 12)² + ( x − 0)² 100 = x² − 4x + 4 + x² + x² − 24 x + 144 + x² 100 = 4 x² − 28 x + 148 4 x² − 28 x + 48 = 0 / : 4 x² − 7 x + 12 = 0 Δ = 49 − 4*1*12 = 1

	7 − 1		7 + 1
x =		= 3 lub x =		= 4
	2		2

więc y = 3 lub y = 4 Odp. C = ( 3; 3) lub C = ( 4; 4) =======================

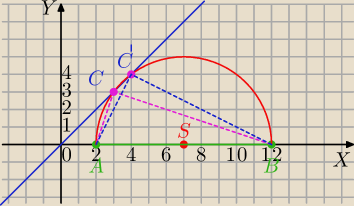
utem: I I sposób AB przeciwprostokatna y=x prosta

	2+12
S=(		,0)=(,0) środek odcinka AB
	2

C∊prostej, y=x ∡C=∡C'=90^o jako katy wpisane w okrąg oparte na średnicy. (x−7)²+y²=5² równanie okręgu o środku(7,0) i r=5 y=x x²−14x+49+x²=25 2x²−14x+24=0 x²−7x+12=0 Δ=49−48=1

	7−1		7+1
x=		=3 lub x=		=4
	2		2

y=3 lub y=4 C=(3,3), C'=(4,4)

Janek191: Ładny rysunek

utem: Hej, to samo wyszło. Lubię rysunki w geometrii.