sss Dve: Chce to zrozumiec, zadanie z funkcji; Funkcja f:R²−>R okreslona jest wzorem f(x,y)=|x|+|y|

	1		2
niech An=[		+1, 4−		]
	n		n

Wyznaczyc Un∊N f⁻¹(An) oraz ∩n∊N f⁻¹(An) Rozpisze mi ktos krok po kroku jak to trzeba zrobic bo kompletnie nie ogarniam tych funkcji dwoch argumentow

Dve: Jest ktos w stanie mi pomoc

Krzysiek: dla ustalonego 'n' f⁻¹(A_n)={(x,y); 1/n+1≤|x|+|y|≤4−2/n } i teraz wydaje mi się,że: ∪n∊N f⁻¹(A_n)={(x,y);1≤|x|+|y|≤4} ∩n∊N f⁻¹(A_n)={(x,y); |x|+|y|=2 } ale lepiej to Sam/a rozrysuj/rozpisz sobie dla kilku 'n'

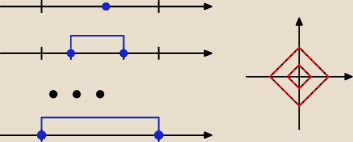
Godzio: Wiemy, że suma i przekrój przeciwobrazu to przeciwobraz sumy i przekroju więc najpierw wysumujemy i przekroimy zbiory A_n (tak chyba łatwiej to zobaczyć) U_nA_n = [1,4] ∩_nA_n = {2} f⁻¹[ (1,4) ] = { (x,y) ∊ R² : 1 ≤ |x| + |y| ≤ 4 } −− to jest ten obszar między dwoma kwadratami (bez obwódek tych kwadratów) f⁻¹[ {2} ] = { (x,y) ∊ R² : |x| + |y| = 2 } −− to jest kwadrat (w pozycji ukośnej tak ja na rysunku do pierwszego podpunktu)