Narysuj wykres funkcji Flap: Narysuj wykres funkcji f(x)=(lsinxl + sinx)cosx. Podaj zbiór wartości wszystkich wartości parametru m, dla których równanie (lsinxl + sinx)cosx=m ma w przedziale <−2π,2π> dokładnie 4 rozwiązania. Mógłby ktoś podać jakąś podpowiedź, jak zabrać się za te zadanie

Bizon: 1^o ... dla 2kπ≤x≤3kπ f(x)=2sinxcosx ⇒ f(x)=sin2x 2^o ... zapisz sobie tam gdzie sinx przyjmuje wartości ujemne f(x)=0

Flap: mógłbyś wyjaśnić to trochę jaśniej

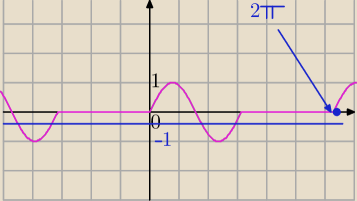
utem: a) f(x)=(lsinxl + sinx)cosx i x∊<−2π,2π> 1) |sinx|=sinx dla x∊<−2π,−π>U<0,π> Wtedy : f(x)=(sinx+sinx)*cosx⇔ f(x)=2sinx cosx⇔ f(x)=sin(2x) 2) |sinx|=−sinx dla x∊(−π,0)U(π,2π) Wtedy: f(x)=(−sinx+snx)*cosx⇔ f(x)=0 b) równanie f(x)=m ma dokładnie 4 rozwiązania w przedziale <−2π,2π>⇔ m∊(−1,0)