Oblicz sinx i cosx Korwin: Oblicz sinx i cosx, jeśli:

	3√5
sinx + cosx =		x∊ (0; π/2)
	5

Wyznaczyłem z tego równania sinus i podstawiłem do jedynki trygonometrycznej, ale z równania kwadratowego wychodzą mi jakieś dziwne liczby..

	2√5		√5
Odp.: sinx =		, cosx =
	5		5

	√5		2√5
lub sinx =		, cosx =
	5		5

ICSP:

	3√5
sinx + cosx =
	5

sin²x + cos²x = 1 Metoda podstawiania :

	3√5
sin2x + (		− sinx)2 = 1
	5

	6√5		9
2sin2x −		sinx +		= 1 // * 5
	5		5

10sin²x − 6√5sinx + 4 = 0 Czy dalej będą problemu ?

Korwin: Nie pomyślałem żebym pomnożyć to równanie przez 5, żeby sobie ułatwić. Dziękuje bardzo

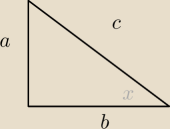Saizou : skoro x jest kątem ostrym to

	a
sinx=
	c

	b
cosx=
	c

−−−−−−−−−−−−−−−−−−−+

	a+b
sinx+cosx=
	c

a+b		3√5
	=		c=√a2+b2 zał b>a
c		5

3√5c=5a+5b 3√5*√a²+b²=5a+5b /² 9*5*(a²+b²)=25a²−50ab+25b² 45a²+45b²=25a²−50ab−25b² 20a²+50ab+20b²=0 /:b²

	a		a		a
20(		)2−50		+20=0 :10		=t
	b		b		b

2t²−5t+2=0 Δ=25−16=9 √Δ=3

	5−3		2		1
t1=		=		=
	4		4		2

	5+3		8
t2=		=		=2 sprzeczność z założeniem
	4		4

a		1
	=
b		2

b=2a c=√a²+4a²=√5a²=a√5

	a		√5
sinx=		=
	a√5		5

	2a		2√5
cosx=		=		jeśli założymy że a>b to otrzymamy drugą wersję
	a√5		5

dłuższy sposób, ale działający