co dalej zrobić w tym zadaniu
Matt: Dla jakich wartości parametru m, równanie √x2+4x+4=|m−3| ma dwa różne pierwiastki ujemne?
po lewej stronie równania jest wzór skróconego mnożenia, no i powstanie |x−2|=|m−3|, i co dalej
z tym zrobić ?
28 gru 22:41
Ajtek:
|x+2| jeżeli już.
28 gru 23:14
pigor: ..., dalej np. tak :
|x+2|= |m−3| ⇔ x+2= −m+3 v x+2= m−3 ⇔
x= −m+1 v x= m−5,
więc warunki zadania będą spełnione
⇔ −m+1≠m−5 i −m+1<0 i m−5<0 ⇔ 2m≠6 i m>1 i m<5 ⇔
⇔ m≠3 i 1<m<5 ⇔
1<m<3 v 3<m<5 ⇔
m∊(1;3} U (3;5) .

−−−−−−−−−−−−−−−−−−−−−−−−
inny sposób podnieś obustronnie /
2 i układ : Δ>0 i x
1x
2>0 i x
1+x
2<0.
28 gru 23:40
Maslanek: A nie może być też na odwrót pigor?

28 gru 23:42
Maslanek: i jesli byśmy podnieśli do kwadratu, to tylko x
1x
2<0 + Δ>0

28 gru 23:42
Ajtek:
Maslanek nie siej fermentu

. Dwa rozwiązania ujemne to x
1x
2 nie może być mniejsze od
zera

.
Cześć Wam

.
28 gru 23:44
Maslanek: Aa...

Myslałem, że różnych znaków xD
28 gru 23:47
Ajtek:
Bb... gapa

28 gru 23:50
utem:
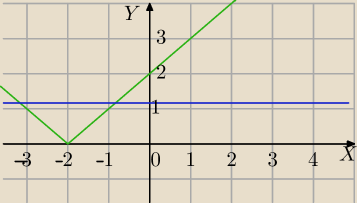
Metoda graficzna:
√x2+4x+4=|m−3|⇔
|x+2|=|m−3|
f(x)=|x+2|
y=|m−3|
Równanie |x+2|=|m−3| ma dwa rozwiązania ujemne⇔
|m−3|>0 i |m−3|<2⇔
m∊R\{3} i −2<m−3<2 /+3⇔
m∊R\{3} i m>1 i m<5⇔
m∊(1,5)\{3}
29 gru 16:07
 −−−−−−−−−−−−−−−−−−−−−−−−
inny sposób podnieś obustronnie /2 i układ : Δ>0 i x1x2>0 i x1+x2<0.
−−−−−−−−−−−−−−−−−−−−−−−−
inny sposób podnieś obustronnie /2 i układ : Δ>0 i x1x2>0 i x1+x2<0.


 . Dwa rozwiązania ujemne to x1x2 nie może być mniejsze od
zera
. Dwa rozwiązania ujemne to x1x2 nie może być mniejsze od
zera  .
Cześć Wam
.
Cześć Wam  .
.
 Myslałem, że różnych znaków xD
Myslałem, że różnych znaków xD

 Metoda graficzna:
√x2+4x+4=|m−3|⇔
|x+2|=|m−3|
f(x)=|x+2|
y=|m−3|
Równanie |x+2|=|m−3| ma dwa rozwiązania ujemne⇔
|m−3|>0 i |m−3|<2⇔
m∊R\{3} i −2<m−3<2 /+3⇔
m∊R\{3} i m>1 i m<5⇔
m∊(1,5)\{3}
Metoda graficzna:
√x2+4x+4=|m−3|⇔
|x+2|=|m−3|
f(x)=|x+2|
y=|m−3|
Równanie |x+2|=|m−3| ma dwa rozwiązania ujemne⇔
|m−3|>0 i |m−3|<2⇔
m∊R\{3} i −2<m−3<2 /+3⇔
m∊R\{3} i m>1 i m<5⇔
m∊(1,5)\{3}