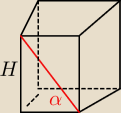
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość p{6}. Prze kamczatka: Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość √6. Przekątna tego graniastosłupa tworzy z płaszczyzną kąt o mierze 60 stopni. Wysokość tego graniastosłupa ma długość: Odpowiedź to 6. chciałem to wyliczyć z funkcji tangesa: tg60=√3

	H
√3=
	√6

	√2
i wychodzi		a powinno wyjść 6
	3

Kaja: źle. to chyba chodzi o kąt miedzy przekątną graniastosłupa a płaszcyzną podstawy, czyli policz kąt między przekątną graniastosłupa, a przekątną podstawy. przekątna podstawy ma długość √6*√2=√12

kamczatka: który to jest kąt ?

Kaja: narysuj przekątną graniastosłupa i przekątną podstawy i zaznacz kąt między nimi

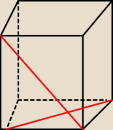
kamczatka: chyba coś tutaj nie tak narysowałem bo dziwnie to wygląda

Kaja: narysuj przekątną graniastosłupa a nie przekątną ściany bocznej

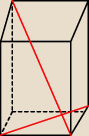
kamczatka: takie coś?

Kaja: niech ta przekątna graniastosłupa zostanie, tylko w podstawie narysuj tą drugą przekątną

Kaja: tak żeby one sie łączyły

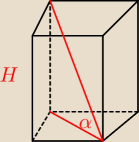
kamczatka: teraz chyba dobrze

kamczatka: tylko jak to teraz obliczyć ?

Kaja: tak. no podobnie jak przedtem

Kaja: tylko przekątna podstawy to √12

kamczatka: wzór na przekątna w graniastosłupie to d=a√2 ? Bo gdzieś widziałem że d=a√3

kamczatka: a nie sory to w sześcianie

kamczatka: ok dzięki wyszło.