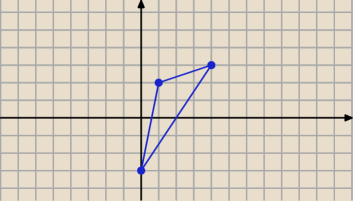
geometria analityczna jerey: wyznaczyć rownanie okręgu opisanego na trójkącie o wierzchołkach A=(0,−3) B=(1,2) C=(4,3)

RS: Układ równań

Eta: 1 sposób o: x²+y²−2ax−2by+c=0 , S(a,b) , r²= a²+b²−c rozwiąż układ trzech równań podstawiając kolejno A(0,−3) : 9+6b+c=0 B(1,2): ......... C(4,3) : ........ 2 sposób: środek okręgu opisanego pokrywa się z punktem przecięcia symetralnych boków trójkąta

RS: :

Eta: ładnie tak się śmiać ?

5-latek: a dlugosc promienia to dlugosc odcinka |AS|=|BS|=|CS|=r

utem: Albo po najlżejszej linii oporu; ( trochę pracochłonne) S(a,b), r− promień okręgu (x−a)²+(y−b)²=r² A=(0,−3) B=(1,2) C=(4,3) te wsp. spełniają równanie okręgu (0−a)²+(−3−b)²=r² (1−a)²+(2−b)²=r² (4−a)²+(3−b)²=r²⇔ a²+9+6b+b²=r² 1−2a+a²+4−4b+b²=r² 16−8a+a²+9−6b+b²=r² prównuję: a²+9+6b+b²=1−2a+a²+4−4b+b²⇔2a+10b=−4 1−2a+a²+4−4b+b²=16−8a+a²+9−6b+b²⇔6a+2b=20 a+5b=−2 3a+b=10 dokończ

Radek: I jak tu wyjdzie r skoro jest a² i b²

MQ: Po wyliczeniu a i b wychodzi z dowolnego z trzech równań −− wystarczy podstawić wyliczone wartości a i b.

Radek: Dzięki.

pl: Czemu w rozwiązaniu utem w tych równaniach przyrównywane jest 1 z 2 i 2 z 3 ?

Mila: Eliminujemy niewiadomą r, Możesz porównać 1 i 2 a potem 1 i 3, też będzie dobrze. Prawe strony są równe r² we wszystkich trzech równaniach.