Geometria analityczna 52: Dane są dwa wierzchołki trójkąta ABC: A=(2,1) i B=(3,−2). Wyznaczyć współrzędne trzeciego wierzchołka wiedząc, że środek ciężkości tego trójkąta leży na osi OX, a pole tego trójkąta jest równe 3.

	51		1		1		1
No i wg moich rozwiązań mam dwie odpowiedzi że C(		,		) v C(		,		) ale
	12		4		4		4

czy obydwie są prawidłowe ? Jakby ktoś mógł to rozwiązać i wyjaśnić.

Panko: Trzy środkowe w Δ przecinają się w jednym punkcie S o współrzędnych S= (x_s,y_s) = ( ( x_A +x_B +x_C)/3 , ( y_A +y_B +y_C)/3 ) Mamy też rozcięcie Δ przez jego środkowe na s z e ś ć trójkątów o równych sobie polach tu równych 3/6 =1/2 Współrzędna środka ciężkości ΔABC to S= ( x_s, y_s)= (x_s,0) → → Pole Δ ASB= 1/2 = 1/2 I det ( SA, SB ) I → → SA =[2−x_s,1] ,SB =[3−x_s,−2] → → Pole Δ ASB= 1/2 = 1/2 I det ( SA, SB ) I 1/2I −2(2−x_s −(3−x_s ) I 1 =I I 3x_s −7 I ⇔ x_s = 8/3 ∨ x_s=2 S= (x_s,y_s) = ( ( x_A +x_B +x_C)/3 , ( y_A +y_B +y_C)/3 ) niech S=(2,0)= ( ( 2+3+x_C )/3 ,( 1−2+y_C )/3 ) stąd oblicz (x_C , y_C) niech S= (8/3,0) =( ( 2+3+x_C )/3 ,( 1−2+y_C )/3 ) stąd oblicz (x_C , y_C)

52: ja robiłem inaczej ale napisz ostateczne wyniki jakie ci wychodzą : ) to sobie sprawdzę...

Eta: Można tak: S−− punkt ciężkości jego współrzędne , to średnia arytmetyczna współrzędnych wierzchołków trójkąta

	1−2+yC
S(x,0) ⇒ yS=		⇒ yC= 1
	3

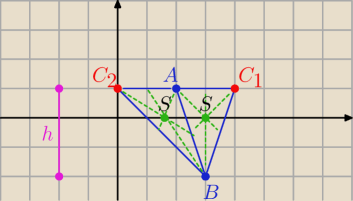
C(x,1) → → Teraz z pola P=0,5|d(AB, AC)|= 3 AB=[1,−3] AC=[x_C−2, y_C−1]= [x−2,0] i mamy: 3*|x−2|= 6 ⇒ |x−2|=2 ⇒ x=4 v x=0 C₁(4,1) , C₂(0,1)

Eta: Podobnie,jak podał Panko ale nieco krócej

52: Eta zobacz ja tak zrobiłem gdzie tu błąd ? http://zapodaj.net/3861ee38bde11.jpg.html

Eta:

	1
SO=		OC
	2

52: faktycznie ajjjj taki błąd <kulka w łeb> Dzięki ; )

Eta:

Eta:

Panko: Zadanie robi się trochę ciekawsze gdy się je zapisze Dane są punkty A , B −−wierzchołki ΔABC i dane jest pole ΔABC i wiadomo, że środek ciężkości ΔABC leży na pewnej ( danej ) prostej. Wyznacz konstrukcyjnie położenie wierzchołka(ów) C ( klasyka−−−linijka bez podziałki + cyrkiel) Wydaje się być prostym.