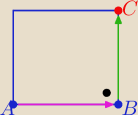
geometria analityczna jerey: dany jest kwadrat ABCD. Kolejne wierzchołki tego kwadratu mają wspolrzedne A=(1,1), B=(5,3). Wyznacz wspolrzedne punktu C rozwiązałem , wyszlo ze C(3,7) < jest ok z odpowiedzią sie zgadza, jednak jest jeszcze 2 wspolrzedna wierzcholka C (7, −1) jak ją odnalezc? najpierw wyznaczylem rownanie prostej ab pozniej rownanie do niej prostopadłej przechodzącej przez punkt b, następnie dlugosc odcinka AB jako promien i rownanie okręgu. i z tego mam uklad rownan. Nie wiem jak wyznaczyc 2 wspolrzedna punktu C, proszę o pomoc. Z gory dzieki.

J: Oznacz szukany drugi punkt np. X. Wtedy punkt B(5,3) bedzie środkiem odcinka XC.

ZKZ: Mozna ja odnalezc np tak masz wspolrzednne punktu (5,3) i wspolrzedne punktu C(3,7) Oznaczmy przez C' wspolrzedna tego punktu co mamy znalezc . Zauwaz ze punkt B(5,3) jest srodkiem odcinka C'C Teraz ze wzorw na srodek odcinka policz wspolrzedne punktu C'

tom: → → → → → AB⊥BC AC=[4,2] to BC=[−2,4] v BC= [2,−4] ( z warunku prostopadłości wektorów BC= [x_C−5, y_C−3] ⇒ x_C−5= −2 i y_C−3=4 v x_C−5= 2 i y_C−3= −4 x_c=3 i y_C= 7 v x_C=7 i y_C=−1 C₁(3,7) , C₂(7,−1)

jerey: dzieki!

tom: Na zdrowie