. Piotr 10: Dla jakich wartości parametru k układ równań (x−4)²+(y−1)²=5 (y−2)*(y−2x+k)=0 ma dokładnie dwa rozwiązania? Wyszła mi taka odpowiedź k∊(−∞;2> ∪ <12;+∞) Jeśli ktoś ma ochotę sprawdzić mi wynik to zapraszam

Piotr 10: I jak ?

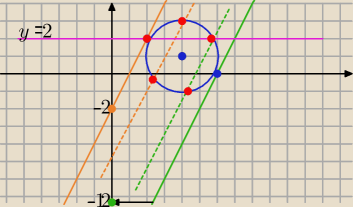
Eta: odp:k∊(2,12)

Eta: Posprawdzaj znaki w Twoim rozwiązaniu

Piotr 10: Bo ja to inaczej zrobiłem trochę w skrócie to tak: (y−2)*(y−2x+k)=0 y=2 v y=2x−k Wstawiając y=2 do pierwszego równania otrzymałem x=6 v x=2 Czyli mam dwa rozwiązania A=(6;2) ; B=(2;2) I teraz wstawiłem y=2x−k do pierwszego równania i otrzymałem 5x²+x(−12−4k)+k²+2k+12=0 I przypadek Δ < 0 −4k²+56k−96 < 0 k∊(−∞;2) U (12;∞) II przypadek 1⁰ Δ=0 2⁰ f(6)=2 1⁰ k=12 v k=2 2⁰ k=12 v k=10 Wiec k=12 III przypadek 1⁰ Δ=0 2⁰ f(2)=2 1⁰ k=12 v k=2 2⁰ k=4 v k=2 Więc k=2 IV przypadek 1⁰ Δ >0 2⁰ f(2)=2 oraz f(6)=2 x∊∅ Sumując to k∊(−∞;2> ∪ <12;+∞) Gdzie jest źle?

Eta: Ja liczyłam 2 przypadek z odległości "d" środka S od prostej 2x−y−k=0 i d< r =√5

Piotr 10: Eta a możesz zerknąć na mój sposób ?

Eta: Słabo widzę ( okulary jeszcze u optyka

Lorak: na pewno Δ < 0 w pierwszym przypadku?

Eta: Dlaczego ... Δ<0? ma być Δ>0

Piotr 10: No tak. Przecież mają być dwa rozwiązania. Więc delta musi być ujemna bo jakby była większa od zera to by były 4 rozwiązania

Eta:

Piotr 10: To jak? Ja będę później jak coś, bo teraz wychodzę

Lorak: Nie przyglądałem się temu zadaniu za bardzo, ale skąd 4 rozwiązania z równania kwadratowego?

Piotr 10: Bo mam już dwa rozwiązania A=(6;2) ; B=(2;2) Może ktoś pomóc?

Lorak: Δ>0 i zapewnić żeby rozwiązania były te same co już masz.

Piotr 10: Uwzględniłem to w 4 przypadku i wyszlo k∊∅ , nic nie rozumiem co mam źle

Lorak: Ale to też już zapewniłeś. Dobrze rozwiązałeś zadanie, Eta musiała się gdzieś pomylić w obliczeniach.

Piotr 10: Ok dzięki za sprawdzenie

Eta: