Układ równań kwadratowych z parametrem
BoosterXS: Wyznaczyć wszystkie wartości parametru m, dla których układ równań
{x
2+y
2=2
{4x
2−4y+m=0
ma dokładnie: a) jedno; b) dwa; c) trzy rozwiązania. Uzasadnić odpowiedź. Rozwiązanie
zilustrować rysunkiem.
Czy mógłby mnie ktoś !naprowadzić! jak zabrać się do tego zadania

28 gru 03:51
Janek191:
x
2 + y
2 = 2 − równanie okręgu o środku O = ( 0; 0) i r =
√2
| | m | |
4 x2 − 4y + m = 0 ⇒ 4y = 4x2 + m ⇒ y = x2 + |
| − równanie paraboli |
| | 4 | |
o wierzchołku W = ( 0;
m4)
Np.a) Okrąg i parabola mają jeden punkt wspólny
m = 4
√2
========
28 gru 09:18
Janek191:
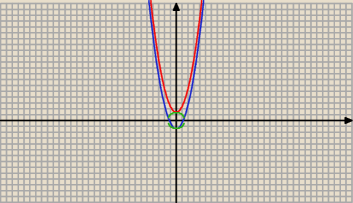
28 gru 09:22
Janek191:
y = x2 + √2 − parabola czerwona
y = x2 − √2 − parabola niebieska
28 gru 09:24
BoosterXS: Czy mógłby mi ktoś jeszcze wytłumaczyć przypadek gdy są dwa rozwiązania.
Pierwsza możliwość to gdy wierzchołek paraboli znajduje się wewnątrz okręgu(na OY) więc gdy
m∊(−4
√2,4
√2), ale czy możliwe jest także takie rozwiązanie, że parabola będzie położona na
OY ale pod okręgiem i może ona mieć 2 punkty styczne z tym okręgiem, a więc 2 rozwiązania

Czy coś takiego zaistnieje, a jeśli tak to dla jakiej wartości parametru m

11 sty 00:26
BoosterXS: Ktoś ma jakiś pomysł?
13 sty 19:06


 Czy coś takiego zaistnieje, a jeśli tak to dla jakiej wartości parametru m
Czy coś takiego zaistnieje, a jeśli tak to dla jakiej wartości parametru m 