Dziedzina funkcji (studia)
Renewerek:
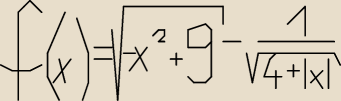
27 gru 23:26
Ajtek:
−x2+9≥0 i 4+|x|>0
Rozwiąż.
27 gru 23:28
Renewerek: Prosze o pomoc w tym przykladzie, nie jestem pewny mojego rozwiazania, nie wiem jak mam to
zrobic.

27 gru 23:29
Renewerek: Nie weim co zrobic z wartoscia bezgledna ... tam bylo cos w liceum, ale ksiazek nie mam

...
27 gru 23:30
Ajtek:
Masz wszystko podane. Skoro jesteś na studiach, to nie powinno to stanowić dla Ciebie problemu.
27 gru 23:30
Ajtek:
3410 kliknij w te cyferki niebieskie. Tam masz wszystko co jest potrzebne do wartości
bezwzględnej.
27 gru 23:32
Renewerek: Dziękuje bardzo

27 gru 23:34
Ajtek:
Powodzenia

.
27 gru 23:34
Renewerek: Mi wyszło
x ≥ 3 ⋀ x ≥ −3 ⋀ x > −4 ⋀x > 4 ,
czyli
chyba od x ε <3;4>
27 gru 23:49
tom:
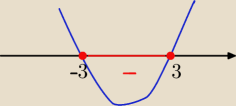
−x2+9≥0 i 4+|x|>0 −−−−ta zachodzi dla x∊R
x2−9≤0
(x−3)(x+3) ≤0 ⇒ x∊<−3,3>
D= <−3,3>
27 gru 23:53
Ajtek:

Nie podoba mi się ten zapis:
x≥3⋀x≥−3⋀x>−4⋀x>4
To jest graficzna ilustracja Twoich przypadków. A to ma być część wspólna. A rozwiązanie jest
błedne.
Rozwiązuj od początku!
27 gru 23:56
Ajtek:
"
tom" pilnuj jabłek
Ety 
27 gru 23:57
Renewerek: hmm bo jak wszedłem w te przykładowe nierówności to tam nie ma takiego przykładu, wiec może
mógłbyś napisać jak to Ci zaszło

?
27 gru 23:58
ZKZ: Wiesz zajsc to mozna ewntualnie w ciaze

4+|x|>0 to |x|>−4 iteraz tak jak jest zawsze lewa strona tej nierownosci ? jak jest
prawa strona ? wiec jaki wniosek
28 gru 00:03
Renewerek: (x−3)(x+3) ≤0
x−3≤0 ⋀ x+3≤0
x≤3 ⋀ x≤−3
D= (− nieskoń. ; −3)
Najlepsze jest to ze z matmy podstawy mialem 86% , a na kolosie z zespolonych i macierzy 37/50

, a takich rzeczy nie potrafie


28 gru 00:04
RS:
Matura nie jest żadnym wyznacznikiem. a poza tym to była banalna matura.
28 gru 00:07
Renewerek: to jakie jest w koncu rozwiazanie, naprawde sam do tego nie dojde

28 gru 00:09
ZKZ: No i powiem CI ze dalej jest zle
Wychodzi na to ze nie umemy rozwiazywac nierownosci kwadratowe

Patrz post 23:53 masz rozwiazanie
28 gru 00:11
Renewerek: napisze mi ktos rozwiązanie czy bedziecie się znęcać nademną

28 gru 00:13
Renewerek: ok ide na wolfram alpha

28 gru 00:15
RS: 
28 gru 00:15
tom:
(x−3)(x+3)≤0 ⇒
x∊<−3, 3>
28 gru 00:15
ZKZ: Popatrz na post 23:53 masz wyznaczona
28 gru 00:16
pigor: ... , ponieważ [n[4+|x| >0 ∀x∊R\\ , to do Df należy tylko taki
zbiór x, że
−x2+9 ≥ 0 ⇔ 9 ≥ x2 ⇔ 3 ≥ |x| ⇔ }x| ≤ 3 ⇔ −3 ≤ x ≤ 3 ⇔ x∊[−3;3]
28 gru 00:17
28 gru 00:19
pigor: ... jeszcze raz zacznę : ponieważ 4+|x| >0 ∀x∊R, to ... i dalej jak wyżej
28 gru 00:19
Renewerek: pigor ale skad wiesz ze 4+|x|>0 zachodzi dla R ?
28 gru 00:20
RS:
Narysuj sobie f(x)=|x|+4czyli rysujesz |x| i przesuwasz o 4 jednostki do góry. I tyle w
temacie.
28 gru 00:22
Renewerek:
28 gru 00:24
Renewerek:
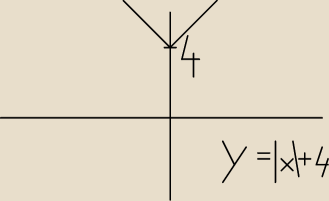
28 gru 00:26
RS:
No i to chyba nie przyjmuje wartości ujemnych a tym bardziej jak przesuniesz do góry. Stąd
oczywista oczywistość.
28 gru 00:26
Renewerek: no okej ale czy z tego wynika x ε R ?
28 gru 00:26
Renewerek: aaa bo patrzymy na iksy ... czyli nie zawiera zadnych iksow i dlatego nie ma ograniczen ...

28 gru 00:27
Renewerek: easy dzieki WSZYSTKIM

szczesliwego nowego roku

28 gru 00:28
tom:
4+|x| >0 4+ liczba nieujemna >0 dla dowolnej liczby "x"
28 gru 00:55
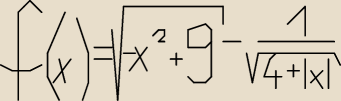

 ...
...

 .
.
 Nie podoba mi się ten zapis:
x≥3⋀x≥−3⋀x>−4⋀x>4
To jest graficzna ilustracja Twoich przypadków. A to ma być część wspólna. A rozwiązanie jest
błedne.
Rozwiązuj od początku!
Nie podoba mi się ten zapis:
x≥3⋀x≥−3⋀x>−4⋀x>4
To jest graficzna ilustracja Twoich przypadków. A to ma być część wspólna. A rozwiązanie jest
błedne.
Rozwiązuj od początku!

 ?
?
 4+|x|>0 to |x|>−4 iteraz tak jak jest zawsze lewa strona tej nierownosci ? jak jest
prawa strona ? wiec jaki wniosek
4+|x|>0 to |x|>−4 iteraz tak jak jest zawsze lewa strona tej nierownosci ? jak jest
prawa strona ? wiec jaki wniosek
 , a takich rzeczy nie potrafie
, a takich rzeczy nie potrafie 


 Patrz post 23:53 masz rozwiazanie
Patrz post 23:53 masz rozwiazanie



 (x−3)(x+3)≤0 ⇒ x∊<−3, 3>
(x−3)(x+3)≤0 ⇒ x∊<−3, 3>

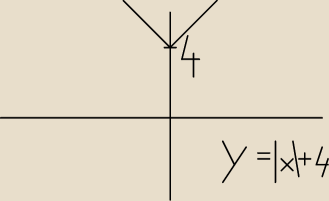

 szczesliwego nowego roku
szczesliwego nowego roku 