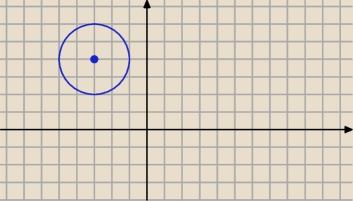
l RS: Wyznacz równania stycznych do okręgu x²+6x+y²−8y+21=0 równoległych do osi Oy . Zrobiłem tak: x²+6x+y²−8y+21=0 (x+3)²−9+(y−4)²−16+21=0 (x+3)²+(y−4)²=4 S=(−3,4) r=2 Te styczne będą miały postać x₁=− oraz x₂=− ale jak to ładnie ''ubrać'' matematycznie ? .

Bizon: ... a np tak współczynnik kierunkowy znasz ... 0 punkty przez które przechodzą te styczne znasz ... więc o co chodzi −

RS: Nie znam tych punktów właśnie ?

RS: Przeczytanie z wykresu nie jest akceptowalnym rozwiązaniem tego zadania.

RS: ?

utem: Odległość stycznej od środka okręgu wynosi 2 i styczna równoległa do OY −3+2=−1 masz styczną m: x=−1, m||OY −3−2=−5 masz styczną n: x=−5, n||OY

RS: Dzięki utem. To nie jest czasami wzór na odległość punktu od prostej ?

ZKZ: Przeciez to jest najlepszy sposob rozwiazania tego zadania jest to dla mnie niezrozumiale jak mozna nie akceptowac tego rozwiazania Chyba ze autor sam sobie tak zalozyl No ale jesli tak zobil to niech liczy ma wspolrzedne punktu S to niech go przesunie o wektor [2 0] i policzy wspolrzedne punktu A a jesli przesunie go o wektor [−2 0] to jak policzy to bedzie mial wspolrzedne punktu B

RS: ZKZ mam podane, że zrobić algebraicznie, dlatego napisałem, że sposób graficzny nie jest akceptowany.

ZKZ: Dobrze

RS: Więc bez zbędnych kłótni