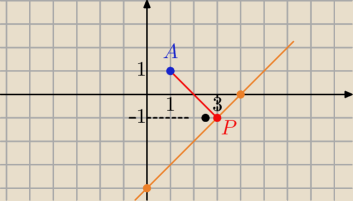
P RS: GeAnality Na prostej o równaniu x− y− 4 = 0 znajdź punkt P , którego kwadrat odległości od punktu A(1,1 ) jest najmniejszy Jak się za to zabrać ? Nie podawać gotowców !

Kaja: jaka postać będzie miał punkt P? jak policzyć kwadrat odległości między tymi punktami? zastanów się

Bizon: ... wyznacz |AP| ... dwie niewiadome ... ale w sumie jedna bo spełniają x−y−4=0 A potem optymalizacja −

RS: x−y−4=0 −y=4−x y=x−4 P(x;x−4) Ale dalej nie bardzo wiem?

Kaja: a wzór na odległość między dwoma punktami znasz? (taki z pierwiastkiem)

RS: Oczywiście, że znam. |AP|=√(x−1)²+(x−4−1)² i potem obu stronie do kwadratu? Wtedy uzyskam |AP|²=równanie kwadratowe ?

Bizon: ... ciepło ... ciepło ...

Kaja: tak.utwórz sobie funkcję: f(x)=(x−1)²+(x−5)², oczywiście odpowiednio ją przekształć. no i policz dla jakiego x ta funkcja przyjmuje najmniejszą wartość

tom:

RS: A ja chcę żeby parzyło. |AP|=√x²−2x+1+x²−10x+25 |AP|=√2x²−12x+26 /² |AP|²=2x²−12x+26 Teraz mam rozwiązać to równanie ?

Kaja: popatrz na mój post z 18:24

tom: x_w= x_min=........

RS: Logiczne,że funkcja kwadratowa skierowana ramionami do góry najmniejszą wartość przyjmuję w x_w ale czemu rozwiązanie równania jest błędnym rozwiązaniem ?

Kaja: a gdzie masz równanie?

Kaja: i jak bys chciał je rozwiązać?

tom: To jest funkcja f(x) =...

RS: @Kaja. |AP|²2=2x²−12x+26 Δ<0 więc nie dałoby się rozwiązać.

RS: @Tom ale ja tutaj nie wiedzę f(x) żeby nazwać to funkcją ?

Kaja: rozwiązujesz równanie z dwiema niewiadomymi licząc deltę?

Kaja: bo funkcję to sobie najpierw utwórz.

Kaja: RS bo u ciebie |AP| to niewiadoma i x to niewiadoma, więc jakim cudem je rozwiązujesz licząc Δ?

RS: Dobra już wiem o co chodziło. Dzięki

pigor: ..., |AP|²= f(x)= 2x²−12x+26= 2(x²−6x+13)= 2*x²−6x+9+4)= 2(x−3)²+8 , więc funkcja f, czyli kwadrat odległości P od A zmiennej x jest f_min= f(3)= 8, dla x=3 zatem P=(x,x−4)= (3,3−4)= (3,−1) − szukany punkt ...