Równania kwadratowe le: Dla jakich wartości parametru m każde z dwóch różnych rozwiązań równania x²−6mx+2−2m+9m²=0 jest większe od 3? Wiem, że delta musi być większa od zera i −b/a>6 czyli wychodzi, że dla każdego m>1 jest spełnione a w odpowiedziach jest m∊(11/9 , +∞)

Kaja: Δ>0 i x₁>3 i x₂>3 x₁−3>0 i x₂−3>0 stąd (x₁−3)(x₂−3)>0 i x₁−3+x₂−3>0 x₁x₂−3(x₂+x₂)+9>0 x₁+x₂−6>0 i teraz zastosuj wzoru Viete'a

Piotr 10: Lub tak 1⁰ Δ > 0 2⁰ f(3) > 0 3⁰ x_w > 3

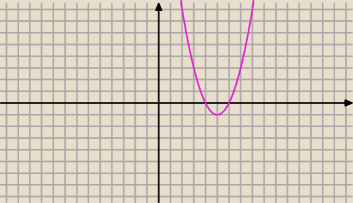
Bizon: ... aby udowodnić "lipę" Twego założenia, że to niby −b/a>6 narysowałem wykres funkcji f(x)=(x−4)(x−6) ... oba pierwiastki są większe od 3 ale wierzchołek jest dla x=5

le: oo stary, mi chodziło o wzory Viete'a, −b/a to to samo co x₁+x₂