Nierówność z wartością bezwzględną. mati555: Witajcie ! Mam mały problem z jednym przykładem z wartością bezwzględną. Wygląda ono następująco : |x−2|+|3x−6|<|x| Ogólnie gdyby nie to, że x jest pod wartością bezwzględną to uznałbym przykład za banalny.

RS: |x−2|+|3x−6|<|x| |x−2|+3|x−2|<|x| 4|x−2|<|x| I teraz przedziały.

Bizon: ... a po co teraz te przedziały ? −

RS: A żeby się pomęczyć dłuższą ścieżką, bo to o czym myślisz nie jest pokazywane w szkole.

mati555: Mój mózg po świętach nie pracuje chyba najlepiej, ale mi wyszło, że x należy do przedziału <8/5,8/3)

Piotr 10: Podnieś do kwadratu najlepiej jest 4Ix−2I < IxI obie strony są dodatnie

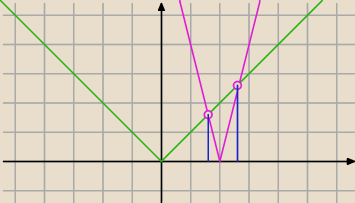
Bizon: ... nie chce mi się liczyć ...ale chyba dobrze −

mati555: Piotrze, ale podnoszenie do kwadratu przy wartościach bezwzględnych (tego typu) jest w mojej opinii chyba bez sensu. Dziękuję Bizonie za odpowiedź, mam nadzieję, że jest tak jak mówisz . Jeszcze jedno pytanko mam. Jak oznaczamy suchy x na osi liczbowej ? Na przykład |x−2| oznaczamy jako 2 lub z innego przykładu |x+2| oznaczamy jako −2.

utem: 4|x−2|<|x| |x−2|=x−2 dla x≥2 |x|=x dla x≥0 Mamy 3 przedziały: 1)x<0 wtedy: 4(−x+2)<−x⇔ −4x+8<−x −3x<−8

	8
x>		i x<0 brak rozwiązania w tym przedziale ( rysuj oś liczbową)
	3

lub 2) x≥0 i x<2 4(−x+2)<x −4x+8<x −5x<−8

	8		8
x>		i x∊<0,2) ⇔x∊(		,2)
	5		5

lub 3) x≥2 4x−8<x 3x<8

	8
x<		i x≥2
	3

	8
x∊<2,		)
	3

odp.

	8		8
x∊(		,		)
	5		3