Trygo Radek: Równania trygonometryczne: Rozwiąż równanie

	1
a) sinx=
	2

b) to samo równanie ale w przedziale <0,2π>

	π		5π
a) x=		+2kπ lub x=		+2kπ k∊C
	6		6

b) mam problem już

Saizou : wiemy że k∊ℤ, zatem dla ◯ k=−1 mamy

	π		5
x=		−2π<0 x=		π−2π<0
	6		6

◯ k=0

	π		5
x=		x=		π
	6		6

◯ k=1

	π		5
x=		+2π>2π x=		π+2π>2π
	6		6

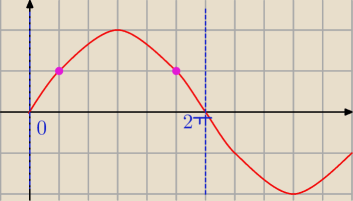
albo prosto z wykresu

Radek: czemu k=−1 k=1 k=0 ?

Saizou : chciałem Ci tylko pokazać że jak pójdziemy w k>0 to przekroczymy 2π, a jak w k<0 to zejdziemy poniżej 0, a dla k=0 nasze wyniki są idealnie w danym przedziale

Radek: Czyli jaka będzie ostateczna odpowiedź ?

Radek: ?

Ajtek: A które x w odpowiedzi Saizou są większe od zera i mniejsze pd 2π

Radek:

Ajtek: Też tak umiem

Radek: Ale ja nie wiem nadal nic ?

Ajtek: Włącz myślenie. a)

	1		π
sinx=		⇒ x=		+2kπ
	2		6

To jest dla Ciebie jasne?

Radek: Tak

Ajtek: Teraz mamy tylko znaleźć rozwiązania z przedziału <0;2π>. Saizou to ładnie rozpisał, pamiętamy, że k∊C. dla k=−1 mamy

	π		11π
x=		+2*(−1)*π=−		a to jest mniejsze niż 0.
	6		6

	5π		7π
x=		+2*(−1)π=−		również mniejsze od zera.
	6		6

dla k=0 policz tym sposobem sam i daj wynik tutaj.

	5π
PS. w poprzednim poście zapomniałem dopisać jeszcze x=		+2kπ
	5

Kejt: i pamiętamy, że tak naprawdę zbiór ℂ to liczby zespolone, natomiast ℤ to liczby całkowite

Ajtek: Kejt hmmmmmm, sio!

Kejt: ja Ciebie też Ajtek no dobra.. idę sobie

Radek: Pisze się k∊C a to, że na studiach tak jest to mało istotne w tym momencie...

Ajtek: Kejt nie idź! Ja tak z czystej symaptii do Ciebie no .

Ajtek: Radek jak idzie?

Radek: Robię zadania ale na razie bez przedziałów zaraz wstawię

Ajtek: Okej .