planimetria
Eta: Zadania z planimetrii
tylko dla
Radka
Na rozgrzewkę
 zad1
zad1 Wykaż,że w trapezie o kątach 30
o i 60
o oraz podstawach a>b
| | a−b | |
długość odcinka łączącego środki podstaw jest równa |
| |
| | 2 | |
zad2 Romb o boku "a" podzielono dwoma półprostymi wychodzącymi
z wierzchołka A kąta ostrego na 3 figury o równych polach.
W jakim stosunku te półproste podzieliły boki rombu?
zad3 W równoległoboku ABCD o kącie ostrym 45
o, na przedłużeniu boku DC
zaznaczono taki punkt M, że AM⊥AB. Wiedząc,że pole tego równoległoboku
jest 1,5 razy większe od pola trapezuABDM.
Wykaż,że |AB|= 3|AM|
Powodzenia

26 gru 17:05
Radek:
Zaraz się za nie zabieram

26 gru 17:09
Radek:
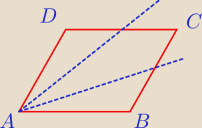
Zadanie 2
Czy rysunek jest ok ?
26 gru 17:17
Eta:
tak

26 gru 17:18
Saizou : tylko dla
Radka 
26 gru 17:23
Radek:
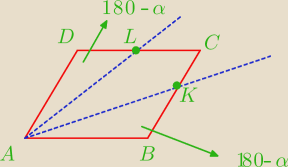
∡D=180−α' ∡B=α ∡C=180−α
bok ma a
Ale dalej nie mam pomysłu
26 gru 17:23
Eta:
@
Radka
Myśl dotąd aż znajdziesz poprawne rozwiązanie !
Na maturze... też napiszesz : "nie mam pomysłu?"

26 gru 17:30
Eta:
@
Saizou .... ja wciąż czekam na rozwiązanie zadania sprzed ... "hoho''

26 gru 17:31
Saizou : pamiętam, ale te zadania są przyjemniejsze

26 gru 17:32
Kejt:  Eta
Eta 
26 gru 17:33
Eta:

26 gru 17:33
Radek:
Tak właśnie napisze

26 gru 17:33
Eta:
No nie

..... to jak uzyskasz 100% ?
26 gru 17:35
Saizou : Eto mogłabyś mi podrzucić link do tych zadań bo nie mogę ich znaleźć

26 gru 17:37
Radek:
Tyle to mogę uzyskać z podstawy. A tutaj bądźmy realistami

A wracając do zadania czy te półproste są równej długości ?
26 gru 17:38
Eta:
Saizou ... szkaj aż znajdziesz ....nie wiem gdzie są

26 gru 17:38
Saizou : gdzieś na forum

26 gru 17:41
Radek:

26 gru 17:44
Eta:

co to za wzór? ... pomyśl troszkę

26 gru 17:51
26 gru 17:52
Ajtek:
Czy BK jest ⊥ do AB?
Eta łap

26 gru 17:54
Eta:
@
Saizou możesz pomóc koledze
Radkowi 
To zad. jest z matury podstawowej

26 gru 18:07
Radek:

z podstawowej

26 gru 18:09
Eta:
Tak, tak

26 gru 18:13
Eta:
Wszystkie są z matury podstawowej

26 gru 18:14
Radek: Dobra to nic tu po mnie

Idę do innych zadań
26 gru 18:15
Eta:
Ejjj .... nie poddawaj się .... walcz do skutku

26 gru 18:16
5-latek: Chcialbym Ci przypomniec ze dzisiaj w nocy robiles zadanie podobne do zadania nr1
26 gru 18:21
Radek:
Ale ja nie wiem jak zrobić to zadanie... Wszystkie pomysły mi się skończyły już...
26 gru 18:21
Saizou :

masz podpowiedź

26 gru 18:22
Eta:
y= a−x x<a

26 gru 18:22
Radek:
a=−x−y
ale co dalej ?
26 gru 18:27
Eta:
a>0 zatem nie może być a= −x−y !
a=x+y
26 gru 18:28
Radek:
I mam pole tego rombu P=x2+2xy+y2
26 gru 18:30
Radek: ?
26 gru 18:42
Eta:
P
1=P
2=P
3 −−− z treści zadania
P(ABCD)= 3P
1
x∊(0,a)
P(ABCD)= a
2*sinα i P
1= a*(a−x)*sinβ= a(a−x)*sinα bo β=180
o−α
dokończ........
26 gru 18:42
26 gru 18:48
Eta:
| | 1 | |
I dalej P1= |
| a*(a−x)*sinα |
| | 2 | |
teraz porównaj te dwie zależności i wyznacz "x" i "a−x"
26 gru 18:54
26 gru 19:04
Eta:
nie!
| a2*sinα | | a*(a−x)*sinα | |
| = |
| |
| 3 | | 2 | |
x=......
26 gru 19:07
Radek:
Czemu nie ?
26 gru 19:08
Eta:
W jakim celu ? i po co?
26 gru 19:10
Eta:
Masz wyznaczyć długości odcinków "x" i "a−x"
26 gru 19:10
Radek:
| a2sinα | | a(a−x)sinα | |
| = |
| /6 |
| 3 | | 2 | |
2a
2sinα=3[a(a−x)sinα]
26 gru 19:14
Eta:
teraz podziel obustronnie przez a*sinα≠0
26 gru 19:14
Radek:
2=3axsinα
26 gru 19:18
Eta:
Przecież sinus się uprościł !
26 gru 19:19
Radek: 2=3ax
26 gru 19:21
Eta:
no i ostatni krok

x=........
26 gru 19:22
26 gru 19:24
Eta:
Źle przekształciłeś w poscie19:21
2a2sinα= 3a(a−x)*sinα
2a= 3a−3x ⇒ x=.....
26 gru 19:28
Radek:
Ma Pani teraz chwilę na równania trygon ?
26 gru 19:41
Eta:
Dokończ najpierw to zadanie .......
26 gru 19:42
Radek:
2a=3a−3x
2a−3a=−3x
−a=−3x
a=3x
26 gru 19:45
Eta:
zatem te półproste dzielą boki rombu w stosunku 2:1
licząc od wierzchołka kąta rozwartego tego rombu
to wszystko

czy to zadanie było trudne?
26 gru 19:48
Eta:
@ pozostałe masz rozwiązać do końca tego roku! ( nie odpuszczę Ci

26 gru 19:49
Radek:
Było trudne. Będą rozwiązane !
26 gru 19:50
Eta:

26 gru 19:50
RS:

Wykaż,że w trapezie o kątach 30
o i 60
o oraz podstawach a>b długość odcinka łączącego środki
| | a+b | |
podstaw jest równa |
| środki podstaw ? Chyba środki boków powinno być ? |
| | 2 | |
28 gru 19:23
Eta:
A to co?

28 gru 19:25
Eta:
środki podstaw kolego !

28 gru 19:25
Saizou : | | a−b | |
Eta]a pierwsze zadanko na pewno ma dobry długość w sensie |
| |
| | 2 | |
28 gru 19:26
Eta:
tak

28 gru 19:27
Eta:
Ot macie "zagwozdkę"

A to takie proste zadanko

28 gru 19:28
Saizou : ja już wie

28 gru 19:29
Eta:
Idę na kisiel

( jak wrócę, zad1/ ma być rozwiązane
28 gru 19:29
Saizou : nie chcę psuć zabawy

28 gru 19:29
Eta:
Saizou poczekajmy na "kozaka"

28 gru 19:30
RS:
I masz babo placek

28 gru 19:34
Eta:
Właśnie jem pyszny "placek"

28 gru 19:36
RS:
Ja nie chciałem planimetrii tylko wektory

Więc nic tu po mnie
28 gru 19:37
Eta:
No to...3zad/ dla
Saizou 
28 gru 19:38
Saizou : to przeprowadź dowód wektorowy

28 gru 19:38
Eta:
A 100% ? (i

będzie

28 gru 19:39
RS:
Easy

Damy radę. Nie od razu Rzym zbudowano.
28 gru 19:39
Eta:
Ja wciąż czekam na rozwiązanie zad.1/ przez "kozaka RS "

28 gru 19:41
RS:

28 gru 19:42
Saizou :
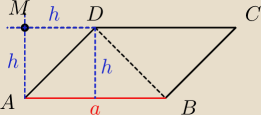
1,5*P
ABDM=P
ABCD
4a=3h+3a
a=3h
ckd
28 gru 19:42
Eta:
c.n.w

28 gru 19:43
Saizou : czepiasz sie

28 gru 19:44
Eta:
Nie, żartowałam

28 gru 19:48
Saizou : 
28 gru 19:53
5-latek: A czy wiemy kto to byl
żółwik ?

28 gru 19:58
Eta:
Wiemy, wiemy

28 gru 19:59
Saizou : to co mogę to pierwsze zadanko

29 gru 13:23
RS:
Możesz.
29 gru 13:23
Saizou : a zapomniałem że to zadanko dla Ciebie
RS 
29 gru 13:26
Saizou : Etuś mogę ?
29 gru 19:31
29 gru 19:38
 zad1 Wykaż,że w trapezie o kątach 30o i 60o oraz podstawach a>b
zad1 Wykaż,że w trapezie o kątach 30o i 60o oraz podstawach a>b


 Zadanie 2
Czy rysunek jest ok ?
Zadanie 2
Czy rysunek jest ok ?





 Eta
Eta 


 ..... to jak uzyskasz 100% ?
..... to jak uzyskasz 100% ?

 A wracając do zadania czy te półproste są równej długości ?
A wracając do zadania czy te półproste są równej długości ?




 co to za wzór? ... pomyśl troszkę
co to za wzór? ... pomyśl troszkę 

 To zad. jest z matury podstawowej
To zad. jest z matury podstawowej 
 z podstawowej
z podstawowej 


 Idę do innych zadań
Idę do innych zadań

 masz podpowiedź
masz podpowiedź 

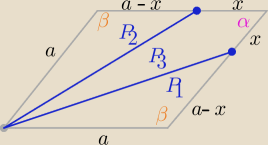
 P1=P2=P3 −−− z treści zadania
P(ABCD)= 3P1
x∊(0,a)
P(ABCD)= a2*sinα i P1= a*(a−x)*sinβ= a(a−x)*sinα bo β=180o−α
dokończ........
P1=P2=P3 −−− z treści zadania
P(ABCD)= 3P1
x∊(0,a)
P(ABCD)= a2*sinα i P1= a*(a−x)*sinβ= a(a−x)*sinα bo β=180o−α
dokończ........
 x=........
x=........
 czy to zadanie było trudne?
czy to zadanie było trudne?


 Wykaż,że w trapezie o kątach 30o i 60o oraz podstawach a>b długość odcinka łączącego środki
Wykaż,że w trapezie o kątach 30o i 60o oraz podstawach a>b długość odcinka łączącego środki




 A to takie proste zadanko
A to takie proste zadanko 

 ( jak wrócę, zad1/ ma być rozwiązane
( jak wrócę, zad1/ ma być rozwiązane




 Więc nic tu po mnie
Więc nic tu po mnie


 będzie
będzie 
 Damy radę. Nie od razu Rzym zbudowano.
Damy radę. Nie od razu Rzym zbudowano.


 1,5*PABDM=PABCD
1,5*PABDM=PABCD








