plan

plan Radek: Kąt ostry wyznaczony przez dwa promienie ma miarę... Oblicz miarę kąta ostrego które tworzą styczne do okręgu poprowadzone przez końce tych promieni Proszę o rysunek.

25 gru 23:23

Radek:

25 gru 23:33

Radek: ?

25 gru 23:41

zvx:

25 gru 23:43

Radek: Dziękuję Pani Eto można jeszcze prosić o pomoc w 5 zadaniach ?

25 gru 23:44

zvx: Dawaj zadanka emotka

25 gru 23:49

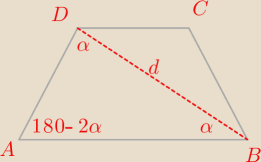
Radek: rysunek

Przekątna trapezu równoramiennego ma długość d i tworzy z podstawami kąt α. Oblicz długości odcinka łączącego środki ramion

d		AB
	=
sin2α		sinα

ABsin2α=dsinα

	dsinα
AB=
	sin2α

A jak DC ?

25 gru 23:56

Radek: Dwa posty znikły ? Czemu ?

26 gru 00:00

Radek:

26 gru 00:12

Radek: Rysunek zły jest (źle kąty ) więc i rozwiązanie złe emotka

26 gru 00:14

Eta:

	a+b
\|EF\|=
	2

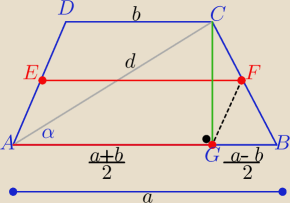
	a+b
Z trójkąta AGC wyznacz		=.....
	2

26 gru 00:17

Radek:

	a+b
\|CG\|²=d²−(		)²
	2

	a²+2ab+b²
\|CG\|=d²−
	4

	d²(a+b)²
\|CG\|²=
	4

	d\|a+b\|
\|CG\|=
	2

	d(a+b)
CG=		?
	2

26 gru 00:24

5-latek: Wiesz czemu jest rowna linia srodkowa w trapezie ?

26 gru 00:26

Radek:

a+b
	=d lina łącząca środki ramion
2

26 gru 00:27

Eta: Nie ! z funkcji trygonometrycznej cosα= .......

26 gru 00:27

Eta: A "małolatek" czemu jeszcze nie śpi

26 gru 00:28

5-latek: Witam emotka

Bo mamusia polozyla w dzien spac emotka

26 gru 00:31

Radek: cos90−α=sinα

	a+b
(		)²=d²+\|CG\|²−(2dCG*sinα) ?
	2

26 gru 00:32

bezendu: 5−latek to idź na

26 gru 00:33

Eta: Echh Radek ( chyba zmęczony jesteś?

	\|AG\|
cosα=		⇒ \|AG\|=\|EF\|= d*cosα
	d

i tyle

26 gru 00:37

Radek: O to chodziło emotka

ehh A zmęczony nie jestem.. Trzeba robić zadania emotka

26 gru 00:38

5-latek: bezendu chetnie bym poszedl ale u mnie na wiosce zabawa dopiero w sylwestra Poza tym przegrywam walke z cukrem i nawet nie moge samochodem jechac do Ziębic aby sie pobawic emotka

26 gru 00:39

Radek: Dobra dziś koniec. Dziękuję i dobranoc emotka

26 gru 00:44

5-latek: Skoro jestes na forum Eta emotka

to prosze spojrz na ten post https://matematykaszkolna.pl/forum/228924.html Wiem ze to nie Ciebie osobiscie ale kiedy pisalem nie bylo Cie na forum Wiec jesli znasz odpowiedz na to moje pytanie to z gory dziekuje za odpowiedz emotka

Pytalem tez kiedys krystek emotka

pozdrawiam no ale niestety nie zna odpowiedzi Przepraszam Radka ze sie wcinam emotka

26 gru 00:52

5-latek: No coz . Wiem ze ciezki problem bo nie kazdy zna ta serie.

26 gru 01:23

Eta: Przykro mi, ale nie znam tej serii emotka

26 gru 01:33

5-latek: Dziekuje za odpowiedz emotka

Moze pozniej zapytam Mile

26 gru 01:36

utem: Witajcie kochani emotka

. Do 5−ciolatka, nie znam tej pozycji literatury.

26 gru 15:39

5-latek: Dziekuje Milu za odpowiedz. emotka

Pewnie bedzie ciezko znalezc . W linku co podal Ajtek tez nie ma .

26 gru 16:47