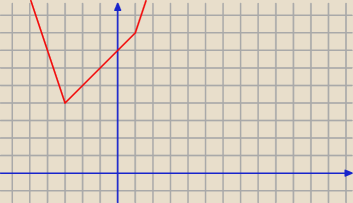
Aksjomat bezendu: Wyznacz najmniejszą wartość funkcji f(x)=|2x+6|+|x−1| f(x)=2|x+3|+|x−1| 1⁰ (−∞,−3) f(x)=−3x−5 2⁰ <−3,1) f(x)=x+7 3⁰ <1,∞) f(x)=3x+5 Narysowałem funkcję w przedziałach i wartość min=4 dla x=−3 Ale czy można to jakoś zrobić bez rysowania wykresu ?

bezendu: I jeszcze jedno pytanie jak wykazać, że każda liczba nieparzysta n³−n jest podzielna przez 24 ? n³−n (n−1)n(n+1) ale to mam cechę podzielności przez 6 max ?

ICSP: f(x) = |2x + 6| + |x−1| Wystarczy policzyć wartości funkcji w punktach x = −3 oraz x = 1 i wybrać mniejszą. 2. n jest nieparzyste, wiec można je zapisać w postaci ....

bezendu: 2. ?

ICSP: ja możesz zapisać każdą liczbę nieparzystą. Było na forum wiele razy.

bezendu: 2n+1 ? Ale co to daje ?

ICSP: Podstaw

ICSP: n = 2k + 1 gdzie k ∊ C Przy takim warunku ma zachodzić : 24 | n³ − n

bezendu: Dobra już widzę, nie było pytania. Dziękuję

Saizou : to zadanie na pewno jest dobrze przepisane? nie powinno być Wykaż, że dla każdej liczby nieparzystej n liczba w postaci n³−n jest podzielna przez 24 .