fgh nnn: Dlugosci krawedzi prostopadloscianu sa kolejnymi liczbami naturalnymi. przekatna prostopadloscianu ma dl 5√2 Oblicz dlugosci krawedzi prostopadloscianu

Justa: a=x−1 b=x c=x+1 wzór na przkatna to: √a² + b² + c²to (x+1)² +x² + (x−1)² =25*2 =50 x² +2x +1 + x² + x² −2x +1 = 50 3x² = 48 x² =16 x=4 v x=−4 (sprzeczne, poniewaz x>0) a=4−1=3 b=4 c=4+1=5

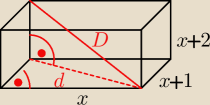
Gustlik: Patrz rysunek, skorzystaj ze wzoru na przekątną prostopadłościanu D²=a²+b²+c², gdzie a, b, c to krawędzie. Ten wzór można łatwo wyprowadzić stosując dwukrotnie tw. Pitagorasa, najpierw obliczyć przekątną podstawy z krawędzi podstawy, a potem przekątną główną D. U ciebie a=x, b=x+1, c=x+2, gdzie x€N.

nnn: Delta mi wychodzi ujemna

nnn: Mozesz napisac swoje obliczenia?

Justa: a=x b=x+1 c=x+2 Tak tak masz napisane w treści zadania D=5√2 D²=a²+b²+c² (5√2)²=x²+(x+1)²+(x+2)² 25*2=x²+x²+2x+1+x²+4x+4 50=3x²+6x+5 3x²+6x−45=0 Δ=b²−4ac Δ=36−4*3*(−45)=36+540=576 √Δ=√576=24

	−b−√Δ		−6−24
x1=		=		=−5 <−− sprzeczne z założenia iż x>0
	2a		6

	−b+√Δ		−6+24
x2=		=		=3
	2a		6

a=3 b=3+1=4 c=3+2=5

nnn: Ale chcialam zrobic z pitagorasa, nie z wzoru