Wyznaczyć cosinus kąta utworzonego przez przekątne - stereometria Dawid: Tak sobie rozwiązuję kilka świątecznych zadanek, które mi przyniósł prawie−mikołaj, prawie−24−ego, w ramach przygotowań do matury rozszerzonej, ale niestety jak narazie średnio mi to idzie, więc mam prośbę do Was o pomoc (: Generalnie mi się nie spieszy, staram się robić wszystko systematycznie i rozumiem, że w święta może być mała aktywność − więc bez spiny, niemniej jak ktoś by znalazł czas rozwiązać je albo pomóc mi w naprowadzeniu na rozwiązanie − wieeelkie dzięki. Wesołych świąt, swoją drogą! 1. Przekątne dwóch sąsiednich ścian bocznych prostopadłościanu nachylone są do płaszczyzny podstawy pod kątami α, β. Wyznacz cosinus kąta utworzonego przez te przekątne. Póki co wyznaczyłem tu jedynie dwa równanka x'a(przekątna podstawy). Z pitagorasa, że x²=b²+a², gdzie a i b to boki podstawy oraz z twierdzenia cosinusów, że x²=y² + z² − 2yzcosγ, gdzie y i z to przekątne ścian bocznych. 2. W graniastosłupie prawidłowym czworokątnym przekątna podstawy ma długość d i tworzy z przekątną ściany bocznej kąt α. Oblicz V graniastosłupa. V=^d2*H₂ gdzie d to przekątna podstawy, a H to bok ściany bocznej. Poza tym widzę tu trójkąt równoramienny o podstawie d, wysokości H no i oczywiście dwóch kątach alfa.

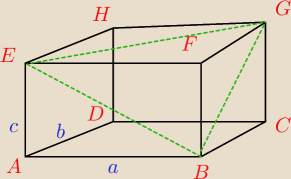
Panko: 1^◯ Oznaczmy trójkę długości krawędzi z wierzchołka A jako : a,b,c I ∡ABEI =α , I∡CBGI =β , I ∡EBGI=γ wtedy IEBI =√c² +a² IBG I= √b²+c² IEGI=√a²+b² γ −−−− kąt utworzony przez te przekątne wtedy dla ΔBEG jest : (a²+b²) =(c²+a²) + (b²+c²) −2√c² +a²√b²+c²cosγ po redukcji c²=√c² +a²√b²+c²cosγ cosγ=c/√c² +a² * c/√b²+c² czytając z rysunku sinα=c/√c² +a² i sinβ=c/√b²+c² ostatecznie cosγ= sinα* sinβ

Dawid: dzięki wielkie, a w drugim może ktoś pomóc?

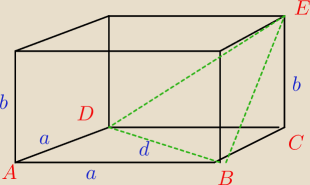
Panko: a− krawędź podstawy ( d=a*√2 ) ; b−−−krawędź boczna Pole podstawy graniastosłupa = 1/2d² Δ DEB jest równoramienny o kącie przy podstawie α ( I∡DBEI=α=I∡BDEI ) oraz IDEI =IBEI =√a²+b² Z Δ DEB jest cosα =a√2/2 / √a² +b² stąd √a² +b² * cosα = a√2/2 b² +a² = a²/ (2*cos²α ) b²= a²*( 1/(2cos²α) −1 ) b²= a² *( 1−2cos²α ) / 2cos²α Teraz kosmetyka ułamka ( 1−2cos²α ) / 2cos²α Korzystam z tożsamości cos²α = 1/( 1+ tg²α) wtedy ( 1−2cos²α ) / 2cos²α = [ 1 − 2/( 1+tg²α) ] /( 2 / (1+tg²α) ) =( tg²α+1 −2)/2 = ( tg²α−1) /2 wracam do wyznaczenia b b²= a² *( 1−2cos²α ) / 2cos²α = a²* ( tg²α−1) /2 stąd b=a*√ ( tg²α−1) /2 = ( d/√2 )*√ ( tg²α−1) /2 = ( d*√tg²α−1 ) /2 Objętość graniastosłupa = ( 1/2 * d²) *d*√ ( tg²α−1) *(1/2) Ostatecznie objętość= (1/4)d³ * √tg²α−1

Dawid: Tu jeszcze dwa zadanka, jakbyś mógł. Zad. 1 Podstawą ostrosłupa jest trójkąt o kątach α, β wpisany w okrąg o promieniu R. Wysokość ostrosłupa jest równa długości boku leżącego na przeciw kąta β. Oblicz V ostrosłupa. Zad.2 Dwie krawędzie ostrosłupa trójkątnego zawierające się w prostych skośnych mają długość b. Zaś długość każdej z pozostałych krawędzi wynosi a. Wyznacz V ostrosłupa. I jeszcze jedno pytanie, znalazłem dzisiaj w sieci taką własność dla równoległoboków(możliwe, że i na tym forum zadaniowym): 2a2+2b2= e2 +f2. Mógłby ktoś mi wyjaśnić z czego to wynika?

Dawid: up, byłbym bardzo wdzięczny jakby ktoś pomógł

pigor: ..., zad.1 podstawą ostrosłupa jest trójkąt o kątach α, β wpisany w okrąg o promieniu R. Wysokość ostrosłupa jest równa długości boku leżącego na przeciw kąta β. Oblicz V ostrosłupa. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− np. tak : (*) V_o=¹₃S_p*H= ?, ale z danych warunków zadania, tw. sinusów

	abc
i wzoru tablicowego na pole trójkąta Sp=		, gdzie:
	4R

b=H=2Rsinβ i a=2Rsinα i c=2Rsin(180^o−(α+β))= 2Rsin(α+β) , czyli

	2Rsinα*2Rsinβ*2Rsin(α+β)
Sp=		= 2R2sinα sinβ sin(α+β), stąd i z (*)
	4R

V_o=¹₃S_p*H= ¹₃* 2R²sinα*sinβ*sin(α+β)* 2Rsinβ, czyli V_o= ⁴₃R³sinα*sin²β*sin(α+β) − szukana objętość ostrosłupa . ...

pigor: ...., a ta własność dla równoległoboków 2a²+2b²= e²+f² wynika np. z ... dwukrotnego użycia tw. cosinusów, mianowicie : dla kąta ostrego α i rozwartego 180^o−α równoległoboku, wtedy masz np. : e²= a²+b²−2abcosα i f²= a²+b²−2abcos(180^o−α) ⇔ ⇔ e²= a²+b²−2abcosα i f²= a²+b²+2abcosα /+ stronami ⇒ ⇒ e²+f²= 2a²+2b² . ... c.n.w. ...