

 Następnie zaznaczasz przestrzeń spełniającą naszą nierówność. Analogicznie
z drugą prostą: zamieniasz na postać kierunkową, rysujesz ją, zaznaczasz przestrzeń
spełniającą nierówność. Gdy masz już określone obie przestrzenie z rysunku, zaznaczasz ich
część wspólną(innym zakreśleniem, kolorem) i masz gotowe rozwiązanie układu nierówności na
układzie współrzędnych.
PS: Która klasa?
Następnie zaznaczasz przestrzeń spełniającą naszą nierówność. Analogicznie
z drugą prostą: zamieniasz na postać kierunkową, rysujesz ją, zaznaczasz przestrzeń
spełniającą nierówność. Gdy masz już określone obie przestrzenie z rysunku, zaznaczasz ich
część wspólną(innym zakreśleniem, kolorem) i masz gotowe rozwiązanie układu nierówności na
układzie współrzędnych.
PS: Która klasa?
 Maturalna, a te zadania sa z nowej ery do rozszerzenia.
Maturalna, a te zadania sa z nowej ery do rozszerzenia.
 Jedynie trzeba uważać na te bezwzględne
Jedynie trzeba uważać na te bezwzględne 
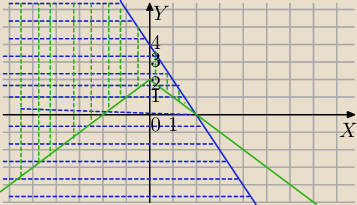 a)
2x + y − 4 ≤ 0
|x| + y ≥ 2 Przekształcam obydwa równania
y≤−2x+4 zbiór wszystkich punktów leżących pod prostą y=−2x+4
y≥−|x|+2 zbiór wszystkich punktów leżących nad wykresem y=−|x|+2
Rozw. część wspólna
a)
2x + y − 4 ≤ 0
|x| + y ≥ 2 Przekształcam obydwa równania
y≤−2x+4 zbiór wszystkich punktów leżących pod prostą y=−2x+4
y≥−|x|+2 zbiór wszystkich punktów leżących nad wykresem y=−|x|+2
Rozw. część wspólna
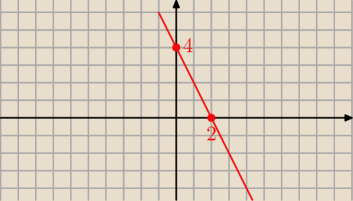 Jest sposób na szybkie narysowanie prostej z równania ogólnego:
Ax+By+C=0
Przenosimy wolny wyraz na prawą stronę równania,
Ax+By=−C
Teraz możemy łatwo obliczyć punkty przecięcia wykresu z osiami:
Jest sposób na szybkie narysowanie prostej z równania ogólnego:
Ax+By+C=0
Przenosimy wolny wyraz na prawą stronę równania,
Ax+By=−C
Teraz możemy łatwo obliczyć punkty przecięcia wykresu z osiami:
| −C | −C | |||
x= | , y= | |||
| A | B |
| 4 | ||
x= | =2 | |
| 2 |
| 4 | ||
y= | =4 | |
| 1 |
| A | B | |||
− | x− | y=1 | ||
| C | C |
| x | y | ||
+ | =1 | ||
| −CA | −CB |
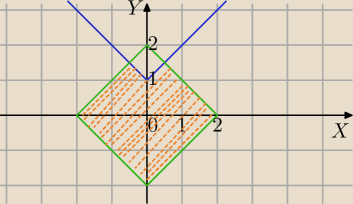 c)
y − |x| ≤ 1
|x| + |y| ≤ 2
y≤|x|+1 zbiór wszystkich punktów leżących pod wykresem funkcji: y=|x|+1
|x| + |y| ≤ 2 zbiór wszystkich punktów leżących na brzegach i wewnątrz kwadratu o
wierzcholkach:
(2,0),(0,2),(−2,0),(0,−2)
rozw. część wspólna
c)
y − |x| ≤ 1
|x| + |y| ≤ 2
y≤|x|+1 zbiór wszystkich punktów leżących pod wykresem funkcji: y=|x|+1
|x| + |y| ≤ 2 zbiór wszystkich punktów leżących na brzegach i wewnątrz kwadratu o
wierzcholkach:
(2,0),(0,2),(−2,0),(0,−2)
rozw. część wspólna
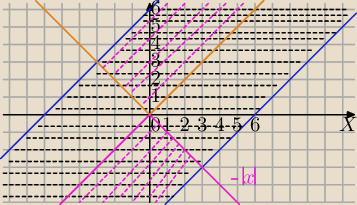 b)
1) |x−y| ≤ 6
2) |y| ≥ |x|
Ad. 1)
x−y≥−6 i x−y≤6⇔
y≤x+6 i y≥x−6 obszar między prostymi ( pas) y=x+6 i y=x−6 łącznie z prostymi
ad2)
|y| ≥ |x|
y≤−|x| lub y≥|x|
b)
1) |x−y| ≤ 6
2) |y| ≥ |x|
Ad. 1)
x−y≥−6 i x−y≤6⇔
y≤x+6 i y≥x−6 obszar między prostymi ( pas) y=x+6 i y=x−6 łącznie z prostymi
ad2)
|y| ≥ |x|
y≤−|x| lub y≥|x|