logarytmy gosiata: rozstrzygnij czy funkcje f i g są równe f(x)= log₃(x−2)− log₃(x−3)

	x−2
g(x)= log3
	x−3

Wg mnie wyszło ze sa równe, ale w odpowiedziach jest odwrotnie. Może ktoś z Was zatem wie jak to zrobić?

5-latek: Odpowiedz sobie najpierw na pytanie Kiedy dwie funkcje sa rowne ?

gosiata: podobnie mam z tym punktem f(x)= logx² g(x)= 2logx proszę o wytłumaczenie

gosiata: są równe wtedy kiedy mają takie same dziedziny

Ajtek: Ustal dziedziny tych funkcji.

5-latek: CO do drugiego zdania zauwaz ze 2logx=logx²

gosiata: f(x)= log3(x−2)− log3(x−3)

	x−2
f(x)= log3
	x−3

x−2
	> 0
x−3

(x−2)(x−3)>0 x=2 x=3 D: x∊ (2;3)

gosiata: no właśnie i w obu tych punktach po uproszczeniu funkcje wyglądają identycznie wiec noo mają chyba te same dziedziny, nie?

5-latek: I oprocz tego ze maja rowne dziedziny to jescze maja te same wartosci funkcji dla argumentow z dziedziny

gosiata: no właśnie. Czyli funkcje powinny być równe, a do obu podpunktów jest w odpowiedziach że nie są rowne,..

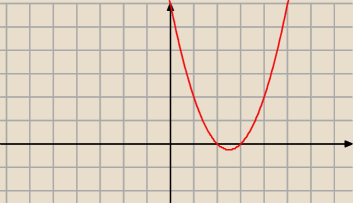
Ajtek: Źle! (x−2)(x−3)>0 masz na rysunku

gosiata: D: x∊ (−nieskonczoności; 2) u(3;+nieskon). Sorkii faktycznie ale nadal dziedziny są te same

Ajtek: Nie są takie same! Wyznacz dziedzinę drugiej funkcji.

gosiata:

	x−2
g(x)= log3
	x−3

no to wychodzi to samo

	x−2
		> 0
	x−3

(x−2)(x−3)>0 D: x∊(−nieskonczoności; 2) u(3;+nieskon).

Ajtek: O funkcję f mi chodzi. Założenia: x−2>0 i x−3>0

5-latek: Gosiu dla 1 funkcji x−2>0 to x>2 x−3>0 to x>3 dziedzina tej 1 to x∊(3,∞)

	x−2
		>0 to x−3 nie rowna sie 0 to x nie rowna sie Ile ?
	x−3

(x−2)(x−3)>0 ranmiona paraboli w gore bo bedzie x² wiec Z tego widzimy ze x nalezy (−oo 2)U(3,oo) maja te same dziedziny czy nie maja ? To bylo do zaadnia nr 1 .

gosiata: yhyyym ; d too tej funkcji najpierw nie mogę sprowadzić do innej postaci? to skoro tak to wtedy x>2 i x>3 więc D: x ∊ (3;+niesk.) ?

5-latek: No dobrze To Ajtek dalej prowadz

Ajtek: Dokładnie tak. Teraz już widzisz wszystko .

gosiata: jejjj rozumiem dziękuje Wam bardzo bardzo bardzo

Ajtek: Zapamiętaj jedną rzecz. Zanim cokolwiek zaczniesz robić z funkcją (nieważne jaka to funkcja), musisz na "dzień dobry" wyznaczyć jej dziedzinę . Przekształcenia po wyznaczeniu dziedziny możesz robić.

gosiata: oki zapamiętam

gosiata: czylii jeszcze jak w tym 2 podpunkcie sie spytam to w f(x) jest dziedzina R a w g(x) x∊ (0,+niesk) ?

Ajtek: f(x) x²>0, popraw dziedzinę

gosiata: D :całkowite?

Ajtek: Zastanów się, wiesz to.

gosiata: noo wydawało mi się, że D:R bo każda liczba spełnia ten warunek ujemna podniesiona do kwadratu jest większa od zera, dodatnia to samo... hmmm

Ajtek: A liczba 0....

gosiata: siet D: R/0

Ajtek: No właśnie. Myśl trochę .

gosiata: dzięki

Ajtek: Powodzenia .