Planimetria
Radek:
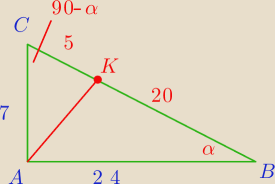
Męczy mnie jeszcze jedno zadnie:
Przyprostokątne AB i AC trójkąta prostokątnego ABC mają długości równe odpowiednio 24 i 7.
Punkt J należy do przeciwprostokątnej trójkąta, przy czym |CK|

KB|=1:4. Oblicz długość
odcinka AK
|AK|=x
|CB|
2=7
2+24
2
|CB|
2=625
|CB|=25
I zgodnie ze stosunkiem 1:4 |CK|=5 |KB|=20
Z twierdzenia cosinusów: cos(90−α)=sinα
x
2=7
2+5
2−(2*7*5*sinα)
x
2=49+25−70sinα
x
2=74−70sinα
x=
√74−70sinα
Ale wynik nie poprawny ?
23 gru 22:14
Radek: A może zapisać pole trójkąta ABC jako sumę pól trójkątów ACK i ABK ?
23 gru 22:18
Radek: Tzn ?
23 gru 22:19
Radek: a odpowiedź jaka jest ?
23 gru 22:28
23 gru 22:30
Radek: to jednak mój pomysł odpada bo źle wychodzi

23 gru 22:39
Radek: Wyszło mi zaraz napiszę

23 gru 22:50
Radek: Ok
23 gru 22:50
Radek: Twierdzenie cosinusow
|AK|2=242+202−2*24*20*(24/25)=2725
|AK|=4√855
23 gru 22:52
 Męczy mnie jeszcze jedno zadnie:
Przyprostokątne AB i AC trójkąta prostokątnego ABC mają długości równe odpowiednio 24 i 7.
Punkt J należy do przeciwprostokątnej trójkąta, przy czym |CK|
Męczy mnie jeszcze jedno zadnie:
Przyprostokątne AB i AC trójkąta prostokątnego ABC mają długości równe odpowiednio 24 i 7.
Punkt J należy do przeciwprostokątnej trójkąta, przy czym |CK| KB|=1:4. Oblicz długość
odcinka AK
|AK|=x
|CB|2=72+242
|CB|2=625
|CB|=25
I zgodnie ze stosunkiem 1:4 |CK|=5 |KB|=20
Z twierdzenia cosinusów: cos(90−α)=sinα
x2=72+52−(2*7*5*sinα)
x2=49+25−70sinα
x2=74−70sinα
x=√74−70sinα
Ale wynik nie poprawny ?
KB|=1:4. Oblicz długość
odcinka AK
|AK|=x
|CB|2=72+242
|CB|2=625
|CB|=25
I zgodnie ze stosunkiem 1:4 |CK|=5 |KB|=20
Z twierdzenia cosinusów: cos(90−α)=sinα
x2=72+52−(2*7*5*sinα)
x2=49+25−70sinα
x2=74−70sinα
x=√74−70sinα
Ale wynik nie poprawny ?

