wielomian marek: Dany jest wielomian W(x) = 2x³ + x + 1 a) Uzasadnij, że wielomian W(x) nie ma dodatnich pierwiastków b) Uzasadnij, że wielomian W(x) nie ma pierwiastków wymiernych c) Twierdzenie: Każdy niezerowy wielomian można przedstawić w postaci iloczynu wielomianów stopnia co najwyżej drugiego Korzystając z podanego twierdzenia uzasadnij, że wielomian W(x) ma co najmniej jeden pierwiastek

Wazyl: b) Twierdzenie o pierwiastkach wymiernych wielomianu, c) wielomian jest stopnia 3 czyli nieparzystego tzn że można przedstawić go za pomocą iloczynu wielomianu stopnia 1 i wielomianu stopnia 2. a) 2x³+x+1=0 x(2x²+1)=−1 Wyrażenie 2x²+1 nigdy nie będzie ujemne. Z tego wniosek że x musi być ujemny.

Wazyl: Jeżeli nie zrozumiałeś c: W(x)=(ax²+bx+c)(x+d)

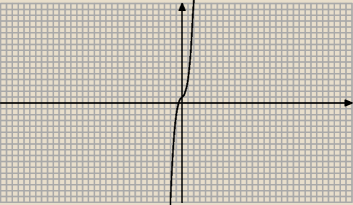
Wazyl: Dowód że wielomian stopnia nieparzystego gdzie k jest stopniem wielomianu i k≥3: Potęga nieparzysta nie zmienia znaku. Jeżeli wsp przed "x" podniesionym do najwyższej potęgi jest dodatni to dla pewnej ujemnej liczby wielomian będzie przybierał wartości ujemne. Dla dodatnich − dodatnie. Wniosek: wykres wielomianu musi przeciąć gdzieś oś OX.

Wazyl: Dowód że wielomian stopnia nieparzystego gdzie k jest stopniem wielomianu i k≥3 ma chociaż jeden pierwiastek: Tak miało byc.