:) Lolka: Punkty A=(6,1) i B=(4,−3) sa dwoma kolejnymi wierzcholkami kwadratu ABCD. Przekotna tego kwadratu jest rowna?

Radek: d=a√2 Oblicz długość odcinka AB

Lolka: jak?

Radek: |AB|=√(4−6)²+(−3−1)²=√4+16=2√5 a=2√5 d=2√5√2 d=2√10

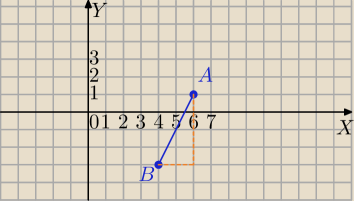
utem: |AB|=√(4−6)²+(−3−1)²=√2²+4²=√4+16=√20=2√5 Najlepiej zaznacz w układzie współrzędnych.

Gustlik: Można bez tego dłuuuuuugiego taaaaaaaasiemcowego wzoru. Wektorem prościej i przejrzyściej: A=(6,1) B=(4,−3) AB^→=[4−6, −3−1]=[−2, −4] a=|AB|=√(−2)²+(−4)²=√4+16=√20=2√5 d=a√2=2√5*√2=2√10

bezendu: Gustlik ale wektorów nie ma na podstawie, więc wzór Mili jest uniwerslany

Gustlik: bezendu, wiem, dlatego pokazuję te wektory, bo warto się tych wektorów nauczyć. Szczerze mówiąc to właśnie bezwektorowe metody (czyli te z podstaw) są trudniejsze. Wektorami wiele zadań idzie rozwiązać dużo szybciej i w dodatku jak jest zadanie złożone z kilku podpunktów, to często za pomocą wektorów idzie obliczyć kilka wielkości naraz nie cofając się do początku. To właśnie na mat−fizie powinny być metody bezwektorowe, bo są trudniejsze i wymagają wiele żmudnych i ciężko przyswajalnych obliczeń.

Radek: Wektory to chyba w geometrii analitycznej ?

Gustlik: Nie tylko, w planimetrii też występują, ale w geometrii analitycznej są [C[NIEZBĘDNE DO PODSTAWOWYCH OBLICZEŃ]], znacznie je skracają i upraszczają więc nie kminię, czemu nie ma ich na podstawie.

Ktoś: A jaka jest u licha Gustliku różnica między zapisem Mili: |AB| = √(4 − 6)² + (−3 − 1)² a twoim zapisem: AB^→ = [4 − 6, −3 − 1] i dalsze Twoje zapisy, przecież to − to samo i gdzie tu widzisz dłuuuuuuuuuuuuuugi taaaaaaaaaasiemcowy wzór. I daj se luz.

cicha noc:

5-latek:

daras: idzie nowe!

5-latek: To jest tak latwe zadanie ze nie powinno w ogole pojawic sie na forum Pojawilo sie chyba tylko dlatego ze autor tego postu albo nie umie liczyc albo mu sie nie chce . Nikogo tu nie obrazam w tej chwili ale tak jest prawda . Wiec dopoki bedziemy rozwiazywac tak proste zadania gdzie trzeba tylko podsatwic do wzoru to beda sie takie dyskusje toczyly Do Ktosia Oczywiscie to jest to samo . Tylko ze czlowiek ktory zna tylko ten wzor na dlugosc odcinka nie bedzie wiedzial ze z tego moze obliczyc wspolczynni kierunkowy prostej przechodacej przez 2 punkty . Jesli zna wektory to bedzie wiedzial .

pigor: ... , a ja sądzę, że jest to zadanie testowe, a autor tego postu zachował dla siebie możliwe 4 odpowiedzi (test jednokrotnego wyboru) ..., szkoda, bo zapewne poprawną odpowiedź można ... "z pamięci" . ...

5-latek: Czesc pigor Tylko ze akuratnie do tego zadsania po co warianty odpowiedzi?

pigor: ... bo mi toto sugeruje to zdanie, cytuję "" Przekotna tego kwadratu jest rowna? " no właśnie ile i tu się proszą 4 odpowiedzi .

5-latek: Zgadza sie i najlepiej ze by odpowiedz 2√10 byla jako a) −−−po co dodatkowy stres

Gustlik: Do 5−latka masz rację − i nie tylko współczynnik kierunkowy, bo z wektorów można obliczyć o wiele więcej rzeczy, np. pola figur, brakujace ich wierzchołki, np. równoległoboku, badać prostopadłość i równoległość prostych itp. bez cofania się do początku i robienia żmudnych obliczeń od podstaw. I dlatego ja uczę wektorów NA PODSTAWACH !

Radek: To mógłby i mnie Pan nauczyć tych wektorów ?

Gustlik: Do Radka − mów mi Gustlik, a nie Pan Co mogą wektory? AB^→=[x_B−x_A, y_B−y_A]=[w_x, w_y] współczynnik kierunkowy

	yB−yA		wy
a=		=		, gdy wx≠0.
	xB−xA		wx

Dla w_x=0 mamy prostą pionową x=x_A, dzieje suię tak, gdy x_B=x_A, oba punkty mają te samą współrzedną x. Długość odcinka |AB|=√x_B−x_A, y_B−y_A=√w_x²+w_y² Np. A=(2, 3) B=(3, 7) AB^→=[3−2, 7−3]=[1, 4]

	4
Wsp. kier. a=		=4
	1

Prosta AB y=4x+b, wstawiam współrzedne np. A i liczę b 3=4*2+b 3−8=b b=−5 y=4x−5 Dł. liczę wykorzystując raz już obliczone współrzędne wektora |AB|=√1²+4²=√17 To tylko namiastka możliwości wektorów. Tu opisałem wykorzystanie wektorów do obliczania pól figur. https://matematykaszkolna.pl/forum/forum.py?komentarzdo=3423 . Pozdrawiam

Gustlik: Oczywiście mialo być |AB|=√(x_B−x_A)²+(y_B−y_A)²=...

Radek: A np da się je wykorzystać jak mam znaleźć prostą styczną do okręgu albo do podobnych zadań ? Bo przy jednokładności bardzo są pomocne

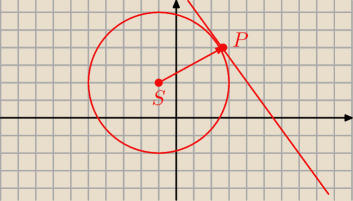
Gustlik: Można, bo promień okręgu jest prostopadły do stycznej. Jeżeli znasz współrzędne środka okręgu S i punktu styczności P, to obliczasz wektor promienia SP^→. Istnieje taki warunek, że wektor o współrzednych [A, B] oraz jego iloczyn przez dowolną liczbę czyli [kA, kB] jest prostopadły do prostej Ax+By+C=0 − https://matematykaszkolna.pl/strona/1214.html. Czyli dwa pierwsze współczynniki równania prostej to współrzędne wektora prostopadłego. Niech np. okrąg ma środek S=(2, 3), a punkt styczności P=(4, 7). Obliczam współrzędne wektora bedacego promieniem okręgu SP^→=[4−2, 7−3]=[2, 4] Czyli styczna jako prostopadła ma równanie 2x+4y+C=0. Podstawiam współrzędne punktu styczności P do tego równania i liczę C: 2*4+4*7+C=0 8+28+C=0 C=−36 Styczna: 2x+4y−36=0 4y=−2x+36 /:4

	1
y=−		x+9
	2

Lub współczynnikiem kierunkowym − II sposób: Wsp. kier. SP

	4
a=		=2
	2

Wsp. kier. stycznej:

	1
a2=−		z warunku prostopadłości prostych
	2

	1
y=−		x+b
	2

	1
7=−		*4+b
	2

7=−2+b b=9

	1
Styczna: y=−		x+9
	2

Gustlik: Tak więc widzisz Radek, wektory znacznie upraszczają i przyspieszają rozwiazywanie wielu zadań z geometrii analitycznej, w tym dziale są one niemal tak samo niezbędne, jak delta w funkcji kwadratowej i powinny być na podstawach, bo rachunek wektorowy jest o wiele łatwiejszy niż bezwektorowe metody obliczeniowe. Jest wręcz banalny.

pigor: ... , ...niech np. okrąg ma środek S=(2, 3), a punkt styczności P=(4, 7). to III sposób S=(2,3), P=(4,7) ⇒ np. PS^→= [2−4,3−7]= [−2,−4]= −2[1,2] ⇒ 1(x−4)+2(y−7)= 0 ⇔ x+2y−18= 0 − szukane równanie stycznej ; −−−−−−−−−−−−−−−−−−−−−−−−−−−− IV sposób S=(a,b) i P=(x_o,y_o), to (x−a)(x_o−a)+(y−b)(y_o−b)= r², czyli tu : (x−2)(4−2)+(y−3)(7−3)= 2²+4² ⇔ 2(x−2)+4(y−3)= 20 /:2 ⇔ ⇔ x−2+2y−6−10= 0 ⇔ x+2y−18=0 . ...