Układ równań z modułem
Wiesiu: Jak rozwiązać taki układ równań? Mi cały czas wychodzi że 1=1 lub 0=0.
22 gru 08:00
rym8: | ⎧ | x+y≥0 | |
| ⎜ | x≥0 | |
| ⎨ | y≥0 |
|
| ⎜ | x + y = 1 | |
| ⎩ | x + y = 1 | |
| ⎧ | y≥−x | |
| ⎜ | x≥0 | |
| ⎨ | y≥0 |
|
| ⎩ | y= 1 − x | |
Podobnie pozostałe przypadki
22 gru 09:28
5-latek: Mozna tez skorzystac z wlasnsci |x+y|≤|x|+|y|
22 gru 10:15
Piotr 10: Ix+yI=1
x+y=1 v x+y=−1
x=1−y
IxI+IyI=1
I1−yI+IyI=1 v I−1−yI+IyI=1
I teraz to rozwiązać wystarczy
22 gru 10:41
Panko: IxI + IyI = Ix+yI I2
x2 +y2 +2I xy I = x2 + y2 + 2xy ⇔Ixy I = xy ⇔ xy ≥0 czyli x, y mają te same
znaki
1◯ x≥0 i y≥0 to x+y=1 stąd y=1−x ≥0 stąd x≤1
czyli x∊[0,1] i y = 1−x
2◯ x≤0 i y≤0 to −x−y=1 stąd y=−1−x ≤0 stąd x≥−1
czyli x∊[−1,0] i y=−1−x
22 gru 16:43
utem:
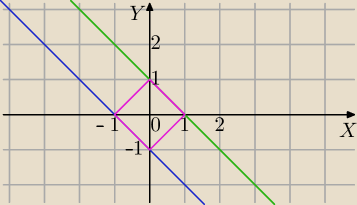
Metoda graficzna:
x+y=1 lub x+y=−1
|x|+|y|=1
⇔
y=−x+1 lub
y=−x−1
|x|+|y|=1
Zbiór rozwiązań:
zbiór par: (x,−x−1) gdzie x∊<−1,0>
lub zbiór par: (x,−x+1) gdzie x∊<0,1>
22 gru 17:34
pigor: ... no to może z interpretacji geometrycznej modułu
do .

mojej "szuflady" jako odległość na osi OX , czyli tu
suma odległości x od 0 −1 v x od 0 i 1) , a więc np. tak :
|x+y|=1 i |x|+|y|=1 ⇔ (x+y= −1 v x+y=1) i |x|+|y|=1 ⇔
⇔ (y= −(x+1) i |x|+|x+1|=1) v (y= −(x−1) i |x|+|x−1|=1) ⇔
⇔ (y= −x−1 i −1≤ x ≤0) v (y= −x+1 i 0≤ x ≤ 1) ⇔
⇔
{(x,y) : x∊[−1;0], y= −x−1} v
{(x,y) : (x∊[0;1], y= −x+1} . ...

22 gru 18:45
 Metoda graficzna:
x+y=1 lub x+y=−1
|x|+|y|=1
⇔
y=−x+1 lub y=−x−1
|x|+|y|=1
Zbiór rozwiązań:
zbiór par: (x,−x−1) gdzie x∊<−1,0>
lub zbiór par: (x,−x+1) gdzie x∊<0,1>
Metoda graficzna:
x+y=1 lub x+y=−1
|x|+|y|=1
⇔
y=−x+1 lub y=−x−1
|x|+|y|=1
Zbiór rozwiązań:
zbiór par: (x,−x−1) gdzie x∊<−1,0>
lub zbiór par: (x,−x+1) gdzie x∊<0,1>
 mojej "szuflady" jako odległość na osi OX , czyli tu
suma odległości x od 0 −1 v x od 0 i 1) , a więc np. tak :
|x+y|=1 i |x|+|y|=1 ⇔ (x+y= −1 v x+y=1) i |x|+|y|=1 ⇔
⇔ (y= −(x+1) i |x|+|x+1|=1) v (y= −(x−1) i |x|+|x−1|=1) ⇔
⇔ (y= −x−1 i −1≤ x ≤0) v (y= −x+1 i 0≤ x ≤ 1) ⇔
⇔ {(x,y) : x∊[−1;0], y= −x−1} v {(x,y) : (x∊[0;1], y= −x+1} . ...
mojej "szuflady" jako odległość na osi OX , czyli tu
suma odległości x od 0 −1 v x od 0 i 1) , a więc np. tak :
|x+y|=1 i |x|+|y|=1 ⇔ (x+y= −1 v x+y=1) i |x|+|y|=1 ⇔
⇔ (y= −(x+1) i |x|+|x+1|=1) v (y= −(x−1) i |x|+|x−1|=1) ⇔
⇔ (y= −x−1 i −1≤ x ≤0) v (y= −x+1 i 0≤ x ≤ 1) ⇔
⇔ {(x,y) : x∊[−1;0], y= −x−1} v {(x,y) : (x∊[0;1], y= −x+1} . ... 