zad madz,: Dany jest trójkąt ABC, gdzie A(−2, 3), B(−2,2), C(2,0). Wyznacz: a) równaniaogólne prostych zawierających boki tego trójkąta b) długości wysokości tego trójkąta

AROB: Pomogę

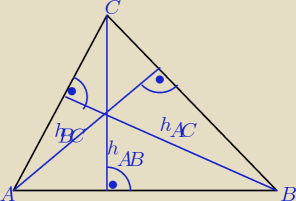
AROB: a) Równanie prostej AB ma postać: x= −2 , ponieważ x_A = x_B = −2. Równanie prostej AC:

	yC − yA
y − yA =		(x − xA)
	xC − xA

	0 − 3
y − 3 =		(x + 2)
	2 + 2

	3
y − 3 = −		(x + 2)
	4

	3		3
y = −		x +
	4		2

Równanie prostej BC:

	yC − yB
y − yB =		(x − xB)
	xC − xB

	0−2
y − 2 =		(x + 2)
	2+2

y − 2 = U{{1}{2}(x + 2)

	1
y =		x + 3
	2

b) Równania wysokości: − Równanie wysokości h_AB ⊥ AB ma postać: y = 0. − Równanie wys. h_BC ⊥ BC , A(−2, 3) :

	1		1
aBC =		, ahBC = −		= −2
	2		aBC

y − y_A = a_hBC(x − x_A) y − 3 = −2(x + 2) y = −2x − 1 − Równanie wys. h_AC ⊥ AC , B(−2,2)

	3		4
aAC = −		, ahAC =
	4		3

y − y_B = a_hAC(x − x_B)

	4
y − 2 =		(x + 2)
	3

	4		14
y=		x +
	3		3

madz,: dziękuje bardzo

AROB: Poprawka prostej BC:

	1
y − 2 = −		(x + 2)
	2

	1
y = −		x + 1
	2

	1
No i to pociąga zmianę w wysokości hBC: aBC = −		, ahBC = 2
	2

y − 3 = 2(x + 2) y = 2x + 7 Przepraszam...

madz,: oki spoczko!