Dwa zadania licealne Maths: Cześć, pomożecie w dwóch zadaniach? 1. Mam 10 ponumerowanych kul. Rozkładamy je losowo w trzech pudełkach. Oblicz prawdopodobieństwo, że w pierwszym będą dokładnie 3 kule. 2. Dany jest trójkąt ABC, na boku AB obrano punkt M taki, że 4|AM|=|AB|, a na boku |BC| obrano punkt N taki, że |BN|=3|NC|. Oblicz w jakim stosunku odcinek |MN| dzieli odcinek |BK|, gdzie K jest dowolnym punktem na boku |AC| Bardzo proszę o pomoc, niezmiernie ważne są te dwa zadania, a obecnie nie wiem jak je zrobić

Maths: Hej, proszę o pomoc...

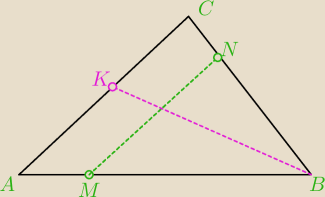
Bizon: ... jeśli przeanalizujesz te proporcje to zauważysz, że AC jest równoległy do MN a trójkąty ABC i MBN są podobne. Dalej już jasne −

pigor: ..., 2. Dany jest trójkąt ABC, na boku AB obrano punkt M taki, że 4|AM|=|AB|, a na boku |BC| obrano punkt N taki, że |BN|=3|NC|. Oblicz w jakim stosunku odcinek |MN| dzieli odcinek |BK|, gdzie K jest dowolnym punktem na boku |AC| . −−−−−−−−−−−−−−−−−−−− 4|AM|=|AB| i |BN|=3|NC| ⇔ (4m=|AB| i |BM|=3m) i (|BN|=3n i |BC|=4n) ⇒

|AB|

4m

3

|BC|

4n

3

⇒

=

=

i

=

=

, stąd

|MB|

3m

4

|BN|

3n

4

i odwrotnego twierdzenia Talesa MN || AC ⇒ ΔMBN∼ΔABC (cecha k,k,k)

	BL		3
i jeśli L punkt przecięcia MN z BK ⇒		=		− szukany stosunek .
	LK		4

Maths: Bizon, jakby było jasne, to by na tym forum się to zadanko nie znalazło Pigor − dzięki wielkie Macie może pomysł na to pierwsze jeszcze, bardzo mi zależy, żeby to wiedzieć, a nie mam do tego odpowiedzi, a nawet obecnie nie wiem do końca jak się za wziąć, choć podejrzewam, że to pewnie dość trywialne zadanko...

Maths:

	3
Ale tak poza tym, to ten punkt K jest dowolny, czyli ten stosunek		jest stały i
	4

niezależny od tego punktu K, dobrze rozumiem?

Panko: I Ω I = 3¹⁰

	10 3
IAI=		* 27

P(A)= IAI / IΩ I

utem: |Ω|=3¹⁰

	10 3
|A|=		*27 wybieramy 3 kule, które maja trafić do pierwszego pudełka, pozostałe 7 kul

rozkladamy dowolnie do pozostałych 2 pudełek.

	10 3   *27
P(A)=
	310

Maths: Ok, mam tylko pytanie mocy przestrzeni, dlaczego 3¹0? Słowo komentarza?

Maths: 3¹⁰

Panko: Dziesięciowyrazowe ciągi których wyrazy to numery pudełek np ( 1,1,1,1,......1) − wszystkie 10 kul jest w pierwszym pudełku ( 2,2,....,2,2,2 ) − wszystkie dziesięć kul jest w drugim pudełku ogólnie (x₁,x₂,x₃,........, x₉, x₁₀ ) , x_i∊{1,2,3} numery pudełek 3* 3 *3 * * 3 * 3 = 3¹⁰

utem: Albo: dla pierwszej kuli możesz wybrać miejsce na 3 sposoby, dla drugiej też na 3 sposoby , dla trzeciej na 3 sposoby ,itd łącznie 3*3*3*..*3=3¹⁰