Rownanie chyba :p Marek: Mam pytanko jest takie zadanie dla jakich wartosci K rownanie Ix² − 4I = K² +1 ma dwa rozne rozwiaznia Wiem ze musi byc Δ >0 oraz x₁x₂ < 0 i teraz jak rozpisac to wartosc bezwzgeldna i to rownanie czy to bedzie : x² − 4 − k² −1 =0 i −x² + 4 − k² − 1 =0 tak jesli dobrze rposze potwoerdzic jesli zle prosze o poprawienie

Marek:

ZKZ: Tylko jeszcze musisz wyznaczyc przedzialy dla ktorych napiszsesz te rownania ale takie x²−4−(k²+1)=0 i drugie −x²+4−(k²+1)=0 jesli chcesz rozwiazac to algebraicznie

Marek: czyli w x²−4−(k²+1)=0 bedzie x ∊ (−∞ ; −2) ∪ (2 ; +∞) a w drugim bedzie x ∊ (−2 ; 2) dobrze mowie

pigor: ..., tak, dobrze, no to baw się dalej swoimi warunkami, tylko nie wiem po co ? − szkoda czasu − daj się przekonać, bo z łatwej analizy wykresu funkcji f(x)=|x²−4| wystarczy rozwiązać nierówność: k²+1>4 ⇔ ⇔ k²>3 ⇔ |k|>√3 ⇔ k<−√3 v k>√3 ⇔ k∊(−∞;−√3)U(√3;+∞) i to tyle...

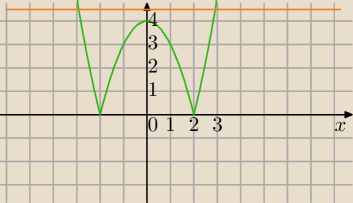
utem: Metoda graficzna: f(x)=|x²−4| zielony wykres Dwa rozwiązania równania: f(x)=k²+1⇔ k²+1>4⇔k²−3>0⇔ dalej jak u pigora