Równania ;-) Mieczysław: Dla jakich wartości m równanie : a) xIx − 1I = m + 1 ma dwa rózne rozwiazania to ja postawilem zaloezenia Δ > 0 x₁x₂ < 0 dobrze one są jak dalej to rozwiazać ?

ZKZ: Tez bym postawil takie zalozenia Tylko ze teraz zrobilbym tak x−1=0 to x=1 to dla x>1 bedzie x²−x=m+1 to x²−x−(m+1)=0 i teraz rowiaz te zalozenia dla x<1 mamy x(1−x)=m+1 to −x²+x−(m+1)=0 i ak samo rozwiaz zalozenia Oczywiscie mozna rozwiazac to tez graficznie

Mieczysław: ale dziwnie wychodzi i cos nie rozumiem

Mieczysław: bo gdy robie Δ > 0 to wychodzi k > − 5/4 a gdy robie x₁x₂ < 0 to wychodzi k < −1 i co dalej drugie tak samo rozwiaze i co dalej ? jak okreslic rozwiaznie

Mieczysław: ojs samiast k powinno byc m (mala literowka)

ZKZ: czego nie rozumiesz ? Definicji wartosci bezwzglednej?

Mieczysław: no ale ja juz rozpisalem to i teraz mam 2 rownania kwadratowe jedno dla x < 1 a drugie dla x ≥ 1 noi rozwiazuje najpierw 1 czyli −X² + x − m − 1 = 0 i do tego Δ > 0 i wychodzi m > − 5/4 pozniej drugie czyli x₁x₂ < 0 to wychodzi m < − 1 i teraz rozwiazac drugie tak samo i jak wziasc odpowiedz ?

Mieczysław: aha okej to wyjdzie to samo w obydwu

Mieczysław: czyli odpowiedz to bedzie k ∊ ( −5/4 ; −1) tak

Mieczysław: no ni eod konca bo mam dylemat

Mieczysław: bo delty wychodza takie same ale gdy rozwazam x₁x₂ < 0 to w 1 wychodzi k <−1 a w drugim k > −1 i teraz jak wziasc odp ze to bedzie zbior rzeczywisty z wylacznie m −1

ZKZ: to zaznacz na osi liczbowej m>−5/4 i m<−1 i wyznacz rozwiazanie

ZKZ: To bedzie do 1 warunku tak samo zrob dla 2 warunku Suma rozwiazan tych 2 warunkow da rozwiazanie tego rownania >

Mieczysław: inaczej bo z 1 rozwniana kwadrat owego wychodzi m ∊ (−5/4 ; −1) a zdrugiego m ∊ (−1 ; +∞) wiec odp bedzie m ∊ (−5/4 ; −1) ∪ (−1 ; +∞)

ZKZ: Skoro takie rozwiazania CI wyszly to tak bedzie odpowiedz .

pigor: ..., dla jakich wartości m równanie x|x−1|=m+1 ma dwa różne rozwiązania ? −−−−−−−−−−−−−−−−−−−−− ...i znowu z łatwej i szybkiej analizy wykresu L−ewej strony danego równania warunki zadania pełnia układ równań : m+1= −¹₄ v m+1= ¹₄ ⇔ m= −1−¹₄ v m= −1+¹₄ ⇔ ⇔ m= −⁵₄ v m= −³₄ ⇔ m∊ {−⁵₄, −³₄} . ...

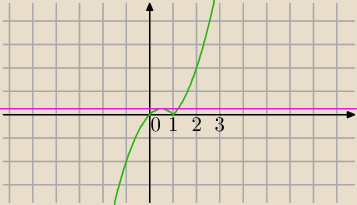
utem: Metoda graficzna : f(x)=x²−x dla x≥1 f(x)=−x²+x dla x<1

	1
xw=
	2

	1
yw=
	4

Dwa różne rozwiązania: 1) m+1=0⇔m=−1

	1		3
2) m+1=		⇔m=−
	4		4

pigor: ..., no tak , znowu kurcze nie wiem skąd mi się wzięło to m+1= − ¹₄ , a miało być przecież m+1=0 , przepraszam.

5-latek: Z poprzedniego przykladu sie wzielo