. Piotr 10: Oblicz długość wektora a^→ − b^→, jeżeli wiadomo, że Ia^→I=6 ,Ib^→I=5, Ia^→+b^→I=4. Proszę o podpowiedź

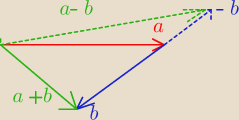
loitzl9006: w tym dużym zielono−niebieskim trójkącie znasz długości boków a+b (4), i całego niebieskiego (10) . szukasz długości a−b jeżeli będziesz znać cosinus kąta pomiędzy a+b, a tym niebieskim to jesteś w domu (bo możesz skorzystać z tw. cosinusów dla dużego trójkąta) wyznaczmy ten cosinus napisz tw. cosinusów dla trójkąta: a, a+b, b (chodzi mi o ten trójkąt z ciągłych linii) tak, aby znaleźć cosinus szukanego kąta jak będziesz miał ten cosinus, to tw. cosinusów dla dużego trójkąta zielono−niebieskiego pozwoli znaleźć długość odcinka a−b jak czegoś nie rozumiesz − pisz

Bizon: √a₁²+a₂²=6 √b₁²+b₂²=5 √(a₁+b₁)²+(a₂+b₂)²=4 √(a₁−b₁)²+(a₂−b₂)²=

Piotr 10: Dobra ok dziękuję wam . W razie problemów będę pisał

Panko: Najkrócej jak można : → → → → gdzie c ◯ d to iloczyn skalarny wektorów c i d ............................................................................ ............................. → → → → → → → → → → I a + b I ²= ( a + b) ◯( a + b) = I a I ² + I b I² + 2* a◯b stąd podstawiając dane jest → → → → 4² = 6² + 5² + 2* a ◯ b ⇒ −45 = 2* a ◯ b → → Obliczamy długość wektora : a − b → → → → → → → → → → I a − b I ²= ( a − b) ◯( a − b) = I a I ² + I b I² − 2* a◯b podstawiamy → → → → I a − b I ²= 6² + 5² − (−45) = 106 ⇒ I a − b I = √106

Piotr 10: Taki sam mi wynik wyszedł. Panko zrobiłem to dwoma sposobami i chyba pierwszy sposób jest najkrótszy wystarczy 2x tw. cosinusów . Ale dzięki też za 3 sposób

Bizon: a w moim też √a₁²+2a₁b₁+b₁²+a₂²+2a₂b₂+b₂²=4 √36+25+2a₁b₁+2a₂b₂=4 ⇒ −2a₁b₁−2a₂b₂=45 do drugiego √a₁²−2a₁b₁+b₁²+a₂²−2a₂b₂+b₂²=√36+25+45=√106