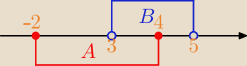
 A więc co widzisz?
A więc co widzisz? 
 Boże co oni teraz w tych szkołach uczą
Boże co oni teraz w tych szkołach uczą
 ... załamka...
... załamka...
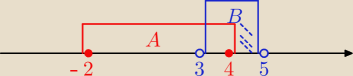 B\A=(4, 5) odp. C.
Kochani − olejcie ten szkolny sposób zaznaczania przedziałów. Szczerze mówiąc przypomina mi on
nieco serial "Sami swoi". Wyobraźcie sobie, że Kargul posadził drzewo na płocie dzielącym go
od Pawlaka i pół drzewka rośnie u Pawlaka, a pół u Kargula. Nietrudno wyobrazić sobie, co by
się wtedy działo − chyba by sie pozabijali o to, czyj to krzak.
I tak samo wygląda ta szkolna Kargulowa metoda − nie wiadomo, na czyim "podwórku", czyli w
którym przedziale znajduje się kropka, bo jest ona zaznaczona na granicy przedziału. Jeżeli
przedział jest domknięty, to kropka powinna być wewnątrz niego, bo jest "nasza", a jeżeli
otwarty − to na zewnątrz, bo jest "sąsiada". Unikniemy wtedy błędów, zwłaszcza przy
wyznaczaniu różnic. Większość uczniów z automatu bierze zamalowaną kropkę za domknięcie
przedziału, a niezamalowaną − za koniec otwarty i w tym przypadku istnieje ryzyko popełnienia
takiego błędu" B\A=<4, 5), a tak widać, że jest (4, 5), bo i 4 i 5 są poza przedziałem,
mimo że 4 jest zamalowana. A jak się właściwie zaznaczy te kropki, wtedy wiadomo, do których
przedziałów one należą, czyli wiadomo, które krzaczki na którym podwórku rosną, czy są "nasze"
czy "sąsiada". Na płocie drzewek się nie sadzi, bo awantura z sąsiadem pewna i tak samo jest z
tymi kropkami.
B\A=(4, 5) odp. C.
Kochani − olejcie ten szkolny sposób zaznaczania przedziałów. Szczerze mówiąc przypomina mi on
nieco serial "Sami swoi". Wyobraźcie sobie, że Kargul posadził drzewo na płocie dzielącym go
od Pawlaka i pół drzewka rośnie u Pawlaka, a pół u Kargula. Nietrudno wyobrazić sobie, co by
się wtedy działo − chyba by sie pozabijali o to, czyj to krzak.
I tak samo wygląda ta szkolna Kargulowa metoda − nie wiadomo, na czyim "podwórku", czyli w
którym przedziale znajduje się kropka, bo jest ona zaznaczona na granicy przedziału. Jeżeli
przedział jest domknięty, to kropka powinna być wewnątrz niego, bo jest "nasza", a jeżeli
otwarty − to na zewnątrz, bo jest "sąsiada". Unikniemy wtedy błędów, zwłaszcza przy
wyznaczaniu różnic. Większość uczniów z automatu bierze zamalowaną kropkę za domknięcie
przedziału, a niezamalowaną − za koniec otwarty i w tym przypadku istnieje ryzyko popełnienia
takiego błędu" B\A=<4, 5), a tak widać, że jest (4, 5), bo i 4 i 5 są poza przedziałem,
mimo że 4 jest zamalowana. A jak się właściwie zaznaczy te kropki, wtedy wiadomo, do których
przedziałów one należą, czyli wiadomo, które krzaczki na którym podwórku rosną, czy są "nasze"
czy "sąsiada". Na płocie drzewek się nie sadzi, bo awantura z sąsiadem pewna i tak samo jest z
tymi kropkami.
 drzwi zamknięte pies siedzi w domu
drzwi otwarte pies uciekł
drzwi zamknięte pies siedzi w domu
drzwi otwarte pies uciekł

 !
!
 udane wyrwanie zęba (powstaje dziura)
zaś
odejmowanie zbioru otwartego to ..
udane wyrwanie zęba (powstaje dziura)
zaś
odejmowanie zbioru otwartego to ..  szczypce ześlizguję się (ząb zostaje) . ...
szczypce ześlizguję się (ząb zostaje) . ... 

 Hehe
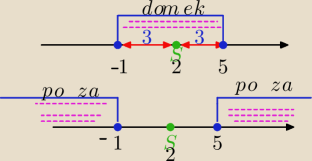
Hehe  Podobnie tłumaczę obrazowo nierówności z modułem:
Byłeś mały(< mniejszy ) siedziałeś w domku i robiłeś kroczki od środka .. od drzwi do drzwi
|x−2|<3 3 kroczki od środka x−2=0 ⇒ x= 2
Jesteś duży ( > większy) poszedłeś na lewo lub na prawo do nieskończoności
Podobnie tłumaczę obrazowo nierówności z modułem:
Byłeś mały(< mniejszy ) siedziałeś w domku i robiłeś kroczki od środka .. od drzwi do drzwi
|x−2|<3 3 kroczki od środka x−2=0 ⇒ x= 2
Jesteś duży ( > większy) poszedłeś na lewo lub na prawo do nieskończoności  |x−2|>3
|x−2|>3
 Ale trzeba pamietac ze i tak wraca sie do domu czyli do srodka(czyli do mamy i taty) nawet
jak jest sie duzym a zwlaszcza jak sie nie za co wypic piwa
Ale trzeba pamietac ze i tak wraca sie do domu czyli do srodka(czyli do mamy i taty) nawet
jak jest sie duzym a zwlaszcza jak sie nie za co wypic piwa 
| a7 | ||
a3=a7−4r, a3= | − chcemy jechać ze stacji nr 7 na stację nr 3 − cofamy się o 4 | |
| q4 |