Geometria analityczna.
zimek: Dany jest okrąg o równaniu: x2−4x+y2+6y=12. Punkty A i B są punktami przecięcia okręgu z
prostą l: 4x−3y−17=0
a) Wyznacz współrzędne punktów A i B.
b) Wykaż, że w prostej l zawarta jest średnica danego okręgu.
Proszę o jakieś podpowiedzi, nie wiem jak ruszyć to zadanie...
20 gru 12:53
ZKZ: | | 4 | | 17 | |
−3y=−4x+17 to 3y=4x−17 to y= |
| x− |
| |
| | 3 | | 3 | |
2 podpowiedz to x
2−4x+y
2+6y−12=0 doprowadz do postaci kanoncznej i przyrownaj te rownania
do siebie i wyznacz punkty przeciecia
20 gru 12:58
J: a) Rozwiązać układ równań (równanie prostej i równanie okręgu)
b) Wykazać, że środek okręgu nalezy do prostej
20 gru 12:59
zimek: zacząłem już wyznaczać sobie x z drugiego równania
20 gru 13:00
Bizon:
... rozwiązuj układ równań ... otrzymasz współrzędne punktów przecięcia
Potem porównaj długość odcinka AB i średnicy okręgu.
20 gru 13:01
J: Propozycja "Bizona" jak najbardziej słuszna,ale czy nie prościej pokazać,że środek okregu
nalezy do prostej ?
20 gru 13:05
zimek: coś mi nie idzie ten układ równań, podstawiam za x 3y/4+17/4 i wychodzą mi jakieś kosmiczne
liczby
20 gru 13:06
ZKZ: Mozna tak i tak
Tak samo jak doprowadzic rownanie okregu w postaci ogolnej do postaci kanonicznej (jak wiele
sie tu nauczy −−pozna wzory skroconego mnozenia) i podstawic do rownania wyliczne y z
rownania prostej i policzyc punkty przeciecia
20 gru 13:09
zimek: raczej tego dalej nie policzę, jeżeli wychodzi mi coś źle w układzie
20 gru 13:13
ZKS:
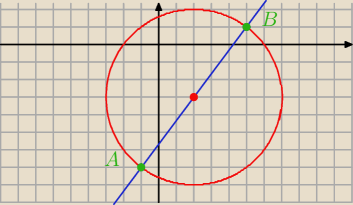
Graficznie.
(x − 2)2 + (y + 3)2 = 52
A = (−1 ; −7)
B = (5 ; 1)
20 gru 13:16
zimek: tak, wiem, że tyle powinno wyjść, pewnie mylę się gdzieś w obliczeniach. możesz to rozpisać?
20 gru 13:19
ZKS:
Rozpisać rozwiązanie graficzne które polega tylko na narysowaniu w jednym układzie
współrzędnych okręgu o równaniu x2 − 4x + y2 + 6y = 12 oraz prostej l : 4x − 3y − 17 = 0?
Jeżeli rozwiązujesz układ równań to pokaż jak to robisz.
20 gru 13:23
zimek: dzięki, zrobiłem juz to graficznie tak jak pokazałeś, nie męcząc układu równań.
20 gru 13:38
ZKZ: no to moze zaproponuje tak
| | 4 | | 17 | |
(x−2)2+( |
| x− |
| +3)2=25 |
| | 3 | | 3 | |
20 gru 13:40
ZKS:
Graficznie ładnie wychodzi i mamy od razu rozwiązanym podpunkt b).
20 gru 13:42
ZKZ: Witam ZKS .
Tylko jedno male ale . A co jesli dostanie polecenie wyznaczyc algebraicznie ,moze nie w tym a
w innym zdaniu ?
To co jak ulamki to klapa?
20 gru 13:47