planimetria
Radek:
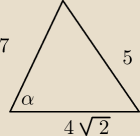
oblicz miarę najmniejszego kąta o bokach długości 4
√2.7.5
5
2=7
2+(4
√2)
2−(2*7*4
√2cosα)
25=32+49−56
√2cosα
−56=−56
√2cosα
cosα=U{
√2{2}
α=45
ale nie należy jeszcze policzyć ze wzorów redukcyjnych cos45
0
cos(90−45)=sin45
√2{2} ?
To samo wyjdzie,ale czy tak powinno sie robić ?
19 gru 22:05
Saizou : a po co ze wzorów redukcyjnych
masz
| | √2 | |
cosα= |
| ⇒α=45o bo α∊(0:90) |
| | 2 | |
19 gru 22:11
matyk: | | √2 | |
Kąt α jest ostry. Wynika z tego, że jeśli cosα= |
| to α=45 stopni. |
| | 2 | |
19 gru 22:12
Radek:
A skąd mam wiedzieć, że to jest trójkąt ostrokątny a nie rozwarty ?
19 gru 22:12
zombi: Największy kąt zawsze znajduje się na przeciwko najdłuższego boku! Dlatego α>90o.
Największy kąt musiałby się znajdować na przeciwko boku 7, a w trójkącie może byc tylko jeden
kąt rozwarty.
19 gru 22:15
Saizou : bo α ma być najmniejsze, a zawsze najmniejszy kąt w trójkącie jest ostry
19 gru 22:15
Eta:
a
2+b
2>c
2 −−−− to trójkąt jest
ostrokątny 
19 gru 22:16
Saizou : Zombi największy kąt w cale nie musi być >90
o 
np. 80
o,60
o,40
o
19 gru 22:17
Eta:

19 gru 22:17
Radek:
W niektórych zadaniach wychodzą po dwa rozwiązania co do kątów. Jak poznać kiedy będą dwa
rozwiązania a kiedy jedno ? Chodzi o kąty
19 gru 22:19
Saizou : np. jak obliczasz z tw. Carnota to otrzymasz np.
| | 1 | |
cosα=− |
| wiesz że jest to kąt rozwarty bo cosα jest ujemny w II ćw. |
| | 2 | |
| | 1 | |
cosα= |
| kąt ostry bo cosα jest dodatni w I ćw. |
| | 2 | |
19 gru 22:21
zombi: Wiem wiem, ale jeśli już pyta o największy to nie na przeciwko boku 5. Dlatego tym bardziej nie
może być rozwarty.

19 gru 22:21
Saizou : 
19 gru 22:23
Radek:
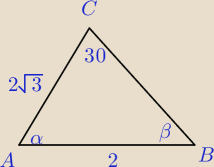
Oblicz miary kątów BAC i ABC jeżelI:
|AB|=2
|AC|=2
√3
|∠ACB|=30
4sinβ=2
√3
β=60
α=180−60−30=60
a w odpowiedziach jest jeszcze druga odpowiedź

19 gru 22:30
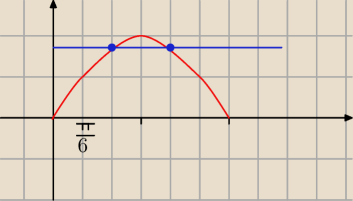
Saizou :
| | √3 | |
sinβ= |
| →β=60o lub β=120o |
| | 2 | |
19 gru 22:33
Saizou :
19 gru 22:35
Radek:
Ze wzorów redukcyjnych ? Ale w pierwszym moim pytaniu też trzeba było tak zrobić ?
19 gru 22:36
Radek: Nie ogarniam tego

19 gru 22:41
Saizou : nie trzeba było bo wiesz że cosx>0 zatem kąt ostry (i miałeś wszystkie boki dane!)
a tutaj liczysz sinx, który w I i II ćw. jest dodatni, zatem musisz rozpatrzeć 2 wersje (nie
masz danych boków)
19 gru 22:42
ZKS:
| | √3 | |
A jak byś rozwiązał równanie trygonometryczne sin(x) = |
| ? |
| | 2 | |
19 gru 22:48
Radek:
| | π | | 2π | |
x= |
| +2kπ lub x= |
| +2kπ |
| | 3 | | 3 | |
k∊C
19 gru 22:51
ZKS:
| | π | | 2 | |
Dlatego β = |
| = 60o ∨ β = |
| π = 120o ponieważ jak wiesz kąty w trójkącie muszą |
| | 3 | | 3 | |
się znajdować w przedziale β ∊ (0 ; 180
o).
Mam nadzieje że wiesz już o co chodzi.
19 gru 22:53
Radek:
Teraz już tak

19 gru 22:55
 oblicz miarę najmniejszego kąta o bokach długości 4√2.7.5
52=72+(4√2)2−(2*7*4√2cosα)
25=32+49−56√2cosα
−56=−56√2cosα
cosα=U{√2{2}
α=45
ale nie należy jeszcze policzyć ze wzorów redukcyjnych cos450
cos(90−45)=sin45
√2{2} ?
To samo wyjdzie,ale czy tak powinno sie robić ?
oblicz miarę najmniejszego kąta o bokach długości 4√2.7.5
52=72+(4√2)2−(2*7*4√2cosα)
25=32+49−56√2cosα
−56=−56√2cosα
cosα=U{√2{2}
α=45
ale nie należy jeszcze policzyć ze wzorów redukcyjnych cos450
cos(90−45)=sin45
√2{2} ?
To samo wyjdzie,ale czy tak powinno sie robić ?

 np. 80o,60o,40o
np. 80o,60o,40o



 Oblicz miary kątów BAC i ABC jeżelI:
|AB|=2
|AC|=2√3
|∠ACB|=30
Oblicz miary kątów BAC i ABC jeżelI:
|AB|=2
|AC|=2√3
|∠ACB|=30



