MNK-Hiperbola
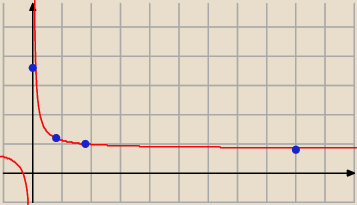
Maliniak: Metodą najmniejszych kwadratów wyznacz funkcję modelową hiperboli dla poniższych danych
x=0,1 y=36,7
x=0,8 y=12,2
x=1,7 y=10.35
x=9 y=8,2
Potrafiłby mi to ktoś jako tako rozwiązać, albo przynajmniej naprowadzić ? Z góry wielkie
dzięki.
18 gru 23:54
19 gru 00:03
daras: wrzuć dane do programu liczącego regresję
19 gru 00:03
Maliniak: Mam podane tylko to co napisałem.
Ten link już przeczytałem, lecz jest on na funkcję liniową a ja mam hiperbolę. Nie wiem czy to
coś zmienia we wzorach końcowych. Muszę zrobić to wszystko ręcznie i pokazać jak doszedłem z
wzoru początkowego (∑[yi−(f(xi)]2=min) do wzoru aproksymacji i z tym mam problem. Później
to pójdzie już z górki.
19 gru 00:29
MQ: Załóżmy, że funkcja ma postać:
Funkcja ϰ
2=∑(y
i−f(x
i))
2
Chcesz znaleźć jej minimum, więc:
(δ tutaj to znak różniczki cząstkowej, bo nie ma w zestawie odpowiedniego).
Dostaniesz układ 3 równań na 3 niewiadome.
19 gru 09:45
Trivial:
MQ, próbowałeś rozwiązać to, co wychodzi z Twoich równań?
| | 1 | |
Dużo łatwiej jest aproksymować funkcjami w bazie: 1, |
| |
| | x | |
Aproksymacja średniokwadratowa
Niech funkcja aproksymująca ma postać
ŷ(x) = c
1φ
1(x) + c
2φ
2(x) + ... + c
Mφ
M(x)
gdzie funkcje φ
1(x), ..., φ
M(x) są znanymi funkcjami bazowymi.
Dla zestawu danych (x
1,y
1), ..., (x
N,y
N) rozwiązanie dokładne (które prawdopodobnie nie
istnieje) musi spełniać następujące równania
y
1 = c
1φ
1(x
1) + c
2φ
2(x
1) + ... + c
mφ
M(x
1)
y
2 = c
1φ
1(x
2) + c
2φ
2(x
2) + ... + c
mφ
M(x
2)
...
y
n = c
1φ
1(x
N) + c
2φ
2(x
N) + ... + c
mφ
M(x
N)
Co można zapisać jako
Φc = y
gdzie
Φ = [ φ
s(x
k) ]
N×M c = [ c
k ]
N×1 y = [ y
k ]
N×1
k = 1, ..., N s = 1, ..., M
Jednakże, dla niezależnych funkcji φ
1(x), ..., φ
M(x) istnieje rozwiązanie przybliżone o
najmniejszym błędzie średniokwadratowym, które jest rozwiązaniem równania
Φc = y → Φ
TΦĉ = Φ
Ty
Aproksymacja średniokwadratowa minimalizuje błąd
ε = ∑
k (y
k − ŷ(x
k))
2
Odnośnie zadania
Wybieramy bazę φ
1(x) = 1, φ
2(x) =
1x. Funkcja aproksymująca ma postać
ŷ(x) = c
1 + c
2(
1x)
Mamy dane:
x = 0.1 0.8 1.7 9
y = 36.7 12.2 10.35 8.2
φ
1 = 1 1 1 1
φ
2 =
10.1 10.8 11.7 19
Φ
TΦĉ = Φ
Ty
21 gru 15:55
