Przeksztalcanie wykresu funcjki sin x Maszyn: Jak powinny wygladac te dwie funkcje −− f{x} = sin|x| f{x} = sin|x− ^pi₄|

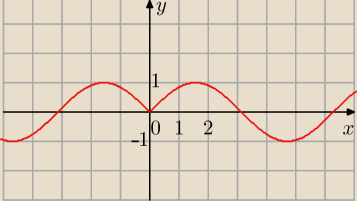
utem: Symetria względem OY tej części wykresu z prawej strony osi Y (z lewej pomijamy)

Maszyn: a moglbym poprosic o male wytlumaczenie dlaczego tak ? Znaczy wiem jak wyglada sin|x| ale nie wiem o co chodzi z |x−^π₄| co tutaj trzeba zrobic bo ^π₄ to 45 stopni wiec trzeba przesunac w prawo o 45 stopni wykres sin|x| ?

zombi:

	pi		pi
Przesuwasz sinx o		w prawo. I teraz zastanów się co zrobi nam |...| na x−		. Przy
	4		4

sin|x| było łatwo, bo dodatnie x zostają natomiast ujemne x zamieniają się dodatnie, więc na identyczną wartość. Dla zobrazowania narysuj sobie wykres funkcji, powiedzmy na to |x−2| Jest to funkcja y=x przesunięta o wektor [2,0], po nałożeniu na nią wartości bezwzględnej Dodatnia część odbija nam się względem x=2, bo weźmy dwa punkty: x=3 wtedy |x−2| = 1 x=1 wtedy |x−2| = 1

	pi
Zatem przy naszym |x−		| będziemy odbijać, 'kopiować' wykres z prawej na lewą względem
	4

	pi
x=
	4

A tutaj jak mi nie wierzysz masz rysunek: http://www.wolframalpha.com/input/?i=sin|x-pi%2F4|

Maszyn: dobrz dziekuje juz rozumiem

utem:

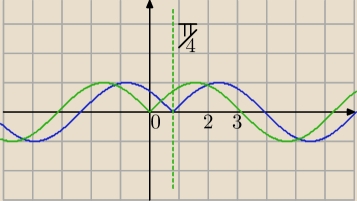
	π
y=sin|x|→T[π/4,0]→y=sin|x−		)
	4

Maszyn: no wlasnie przesunolem sobie asymptote, bo wczesniej tego nie zrobilem i lepiej to zrozumialem. Tylko mam takie male pytanie, czy te dwa pagorki beda sie powtarzaly okresowo?

utem:

	π
Nie są tylko w tym miejscu, dalej sinus i wykres symetryczny względem prostej x=		, tak
	4

jak Ci napisał kolega zombi.