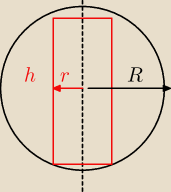
 Problem ma symetrię walcową, więc całkujemy po takich powierzchniach walcowych, jak na rysunku.
Moment bezwładności takiej powierzchni jest równy:
M(r)=m(r)*r2, gdzie M − moment bezwładności, m − masa powierzchni.
m(r)=ρ(r)*2πr*h*dr, gdzie dr − grubość tej powierzchni, ρ(r) − gęstość kuli w odl. r od osi.
h(r)=√R2−r2
ρ(r)=ρ0*r
Trzeba to wszystko poskładać do kupy i wycałkować po dr w granicach od 0 do R.
Problem ma symetrię walcową, więc całkujemy po takich powierzchniach walcowych, jak na rysunku.
Moment bezwładności takiej powierzchni jest równy:
M(r)=m(r)*r2, gdzie M − moment bezwładności, m − masa powierzchni.
m(r)=ρ(r)*2πr*h*dr, gdzie dr − grubość tej powierzchni, ρ(r) − gęstość kuli w odl. r od osi.
h(r)=√R2−r2
ρ(r)=ρ0*r
Trzeba to wszystko poskładać do kupy i wycałkować po dr w granicach od 0 do R.