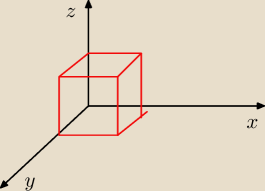
POMOCY CAŁKI Adrian: całka potrójna Obliczyć masę kostki o długości krawędzi równej 2, jeżeli gęstość w każdym punkcie równa jest odległości punktu od podstawy kostki. Mógłby ktoś napisać mi co po kolei trzeba tu zrobić? Bo nie mam zielonego pojęcia jak się za to zabrać

MQ: ρ(x,y,z)=z m = ∫∫∫ ρ(x,y,z) dxdydz = ∫∫∫ z dxdydz = 4∫ z dz Granice całkowania dla każdej zmiennej <0,2>

Adrian: a można sie dowiedzieć tak dokładniej skąd to wynika ∫∫∫ z dxdydz = 4∫ z dz

MQ: Wycałkowałem po dx i dy.

piotrek22: czyli calkujesz po x i po y ? i potem po z ?

Imre: Tutaj nie ma co główkować tylko odrazu przejść do liczenia masy: μdV=μdxdydz czyli: m=∫∫∫μdxdydz m=∭dxdydz

	2 0		2 0		2 0
m=∫		dx∫		dy∫		dz

	2 0		2 0
m=2∫		dx∫		dy

	2 0
m=4∫		dx

m=8